Сборник задач

Охота на
формулу Пика
Автор: Бурлакова Софья
Ученица 9 Б класса
МБОУ «Селенгинской СОШ №2»
2024
Оглавление
| 1. | Введение | 3 |
| 2. | Глава 1. Формула Пика | 4 |
|
| 1.1. Теорема Пика | 4 |
|
| 1.2. Ассоциация для запоминания | 4 |
|
| 1.3. Базовые понятия и теоремы | 4 |
|
| 1.4. Доказательство | 6 |
|
| 1.5. Справедливость формулы | 7 |
|
| 1.6. Исключения | 9 |
| 3. | Глава 2. Задачи | 10 |
|
| 2.1. Решение типовых задач | 10 |
|
| 2.2. Сборник задач | 12 |
|
| 2.2.1. Первый уровень | 12 |
|
| 2.2.2. Второй уровень | 14 |
|
| 2.2.3. Третий уровень | 16 |
|
| 2.3. Проверочная работа | 18 |
| 4. | Заключение | 19 |
| 5. | Список литературы | 20 |
Введение
Уважаемые школьники и учителя!
Эта брошюра является сборником заданий для обучающихся 8-9 классов, кто интересуется математикой, кто желает развить у себя навык работы с фигурами на клетчатой бумаге и тех, кто хочет познакомиться с формулой, которая существенно облегчает решение подобного рода задач.
В различных источниках по подготовке к выпускным экзаменам уделяется много времени решению задач данного типа, но не указывается оптимальный способ их решения. Данный сборник позволит читателю «отточить» навык решения задач на «сетке». Сборник отражает все важные аспекты и их реализацию при обучении способу решения задач.
Задачи сконструированы и подобраны по уровням сложности, что позволяет читателю на нужном ему уровне освоить предложенную теорию. Дана необходимая теория и предложены образцы решения базовых задач.
Глава 1. Формула Пика
1.1. Теорема Пика
Для вычисления площади многоугольника, представленного на линиях сетки можно использовать различные способы. Например, можно достроить фигуру до полного прямоугольника, из которого в дальнейшем вычесть площади лишних фигур, или можно дробить данную фигуру на простейшие и вычислять площадь каждой из них. Но данные способы сопровождаются громоздкими преобразованиями самой фигуры и соответствующими вычислениями.
Рассмотрим ещё один способ, который полезно использовать при нахождении площадей многоугольников.
Теорема (Г. А. Пик). Пусть дан многоугольник на клетчатой основе (сетке). Если число В – это число узлов сетки, расположенных внутри фигуры, а Г – число узлов, расположенных на границе многоугольника, то площадь данного многоугольника вычисляется по формуле: 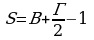 .
.
1.2. Ассоциация для запоминания
 Запомнить формулу Пика удобно через следующий ассоциативный ряд.
Запомнить формулу Пика удобно через следующий ассоциативный ряд.
Для этого можно рассмотреть следующую идею.
Предположим, что мы на наш многоугольник накинули сеть, тем самым, «поймав» фигуру. Для того, чтобы найти площадь, отвечаем на вопрос: Какие узлы я вижу на фигуре? Отвечаем, что видим В - внутренние и Г – граничные узлы. Считаем их. Далее, в формуле располагаем их так: по алфавиту, буква В идёт первой, значит её ставим на первое место 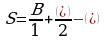 , за ней буква Г, её на второе
, за ней буква Г, её на второе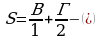 и вспоминаем, что мы на фигуру накинули одну сеть, которую нужно отнять
и вспоминаем, что мы на фигуру накинули одну сеть, которую нужно отнять 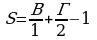 .
.
 1.3. Базовые понятия и теоремы
1.3. Базовые понятия и теоремы
Далее рассмотрим с вами рыболовную сеть. У неё есть вертикальные и горизонтальные прямые, параллельные между собой, которые при пересечении делят плоскость на множество четырёхугольников, которые являются квадратами.
 Квадраты в свою очередь порождают решётку (сетку), а совмещение вершин квадратов образует узлы решётки (сетки). В дальнейшем, площадь одного квадрата сетки мы будем считать равной 1 кв. ед.
Квадраты в свою очередь порождают решётку (сетку), а совмещение вершин квадратов образует узлы решётки (сетки). В дальнейшем, площадь одного квадрата сетки мы будем считать равной 1 кв. ед.
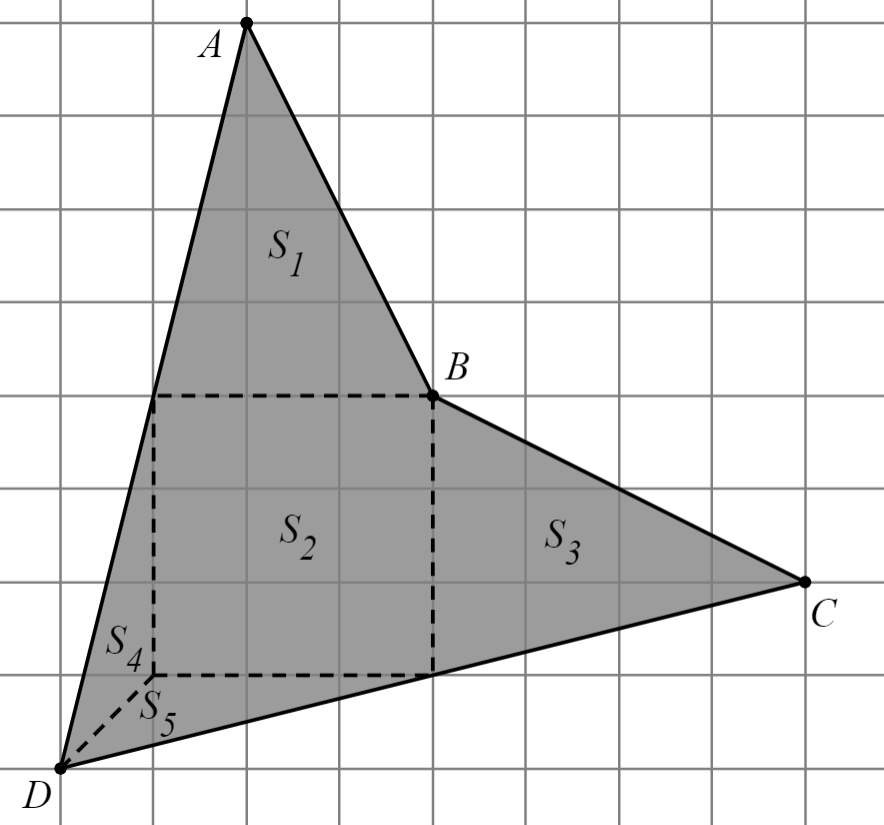
Далее, через каждый узел нашей сетки проведём параллельные прямые. Можем увидеть, что каждый из квадратов разбился на два треугольника. Такой процесс – разбиения многоугольника на непересекающиеся треугольники называется триангуляцией.
Мы будем пользоваться только правильной триангуляцией, а именно случаем, когда два любые треугольника либо имеют общую сторону или вершину, либо не имеют общих точек.
Получаем, что доказав справедливость формулы Пика для треугольников, мы, в силу триангуляции, можем говорить о справедливости формулы Пика для многоугольников.
Для доказательства формулы Пика рассмотрим свойства сетки.
1. Любая прямая, проходящая через два узла сетки содержит в себе бесконечно много узлов сетки и расстояние между любыми двумя соседними узлами, принадлежащими одной прямой, равны между собой;
2. Параллелограмм, построенных на узлах сетки и не содержащий узлов внутри себя и на своих сторонах, называется фундаментальным (элементарным);
3. Треугольник, построенных на узлах сетки и не имеющий других узлов внутри себя и на своих сторонах, называется примитивным (простейшим/элементарным). Легко догадаться, что любой элементарный параллелограмм диагональю разбивается на два элементарных треугольника;
 Теорема. Все элементарные параллелограммы и треугольники между собой имеют равные площади.
Теорема. Все элементарные параллелограммы и треугольники между собой имеют равные площади.
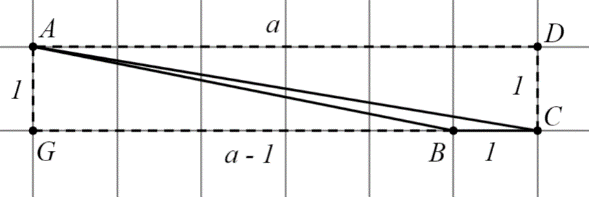
Доказательство: Для доказательства теоремы достаточно показать, что все элементарные треугольники имеют одинаковую площадь. Для этого рассмотрим элементарный треугольник, вокруг которого восстановлен минимальный прямоугольник.
Вычислим площадь треугольника ABC: 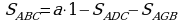 или
или 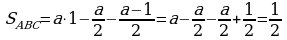 .
.
Ч. т. д.
1.4. Доказательство
Далее, рассмотрим вывод формулы Пика, основанный на подсчёте сумм углов элементарных треугольников.
Д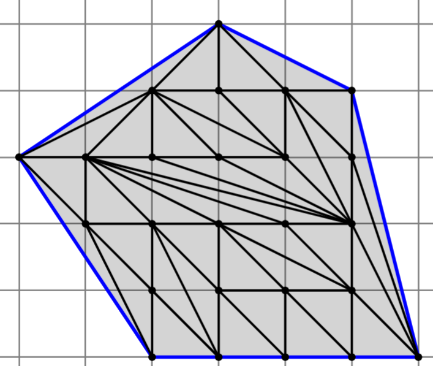 ля вывода формулы рассмотрим произвольный невыпуклый многоугольник у которого
ля вывода формулы рассмотрим произвольный невыпуклый многоугольник у которого 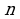 вершин (или как нам привычно - узлов). Узлы на границе фигуры:
вершин (или как нам привычно - узлов). Узлы на границе фигуры: 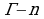 , где Г - это кол-во граничных узлов вместе с вершинами. Буквой N обозначим число элементарных треугольников, на которые мы разбили наш многоугольник. Покажем, что число N не зависит от способа разбиения.
, где Г - это кол-во граничных узлов вместе с вершинами. Буквой N обозначим число элементарных треугольников, на которые мы разбили наш многоугольник. Покажем, что число N не зависит от способа разбиения.
Р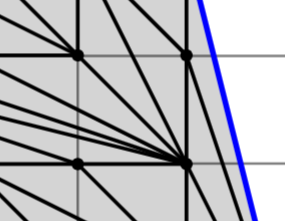 ассмотрим узлы, находящиеся внутри многоугольника, они играют роль вершин треугольников, на которые разбивается многоугольник, заметим, что сумма всех углов, для которых каждая из внутренних точек является вершиной, равна
ассмотрим узлы, находящиеся внутри многоугольника, они играют роль вершин треугольников, на которые разбивается многоугольник, заметим, что сумма всех углов, для которых каждая из внутренних точек является вершиной, равна 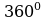 . Получаем, что сумма всех углов всех треугольников с вершинами во внутренних точках равна:
. Получаем, что сумма всех углов всех треугольников с вершинами во внутренних точках равна: 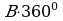 .
.
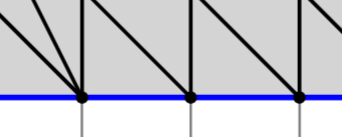 Далее рассмотрим граничные узлы, не являющиеся вершинами, которых
Далее рассмотрим граничные узлы, не являющиеся вершинами, которых 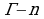 штук. Сумма всех углов всех треугольников при таких вершинах равна:
штук. Сумма всех углов всех треугольников при таких вершинах равна: 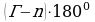 .
.
П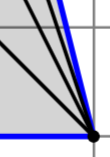 ри вершинах многоугольника, сумма всех углов всех треугольников равна сумме внутренних углов многоугольника, которая вычисляется по известной формуле:
ри вершинах многоугольника, сумма всех углов всех треугольников равна сумме внутренних углов многоугольника, которая вычисляется по известной формуле: 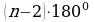 .
.
В общем случае имеем, что сумма всех углов всех треугольников, также равна 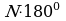 . С другой стороны, учитывая все узлы многоугольника, можно записать равенство:
. С другой стороны, учитывая все узлы многоугольника, можно записать равенство: 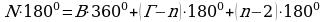 . Преобразовав, получим:
. Преобразовав, получим: 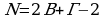 .
.
Вспомним, что площадь элементарного треугольника равна 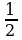 , значит, площадь многоугольника мы с вами найдём из полученной формулы, предварительно разделив её на 2:
, значит, площадь многоугольника мы с вами найдём из полученной формулы, предварительно разделив её на 2: 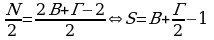 .
.
Ч. т. д.
1.5. Справедливость формулы
Далее покажем, что формула справедлива для произвольных многоугольников.
Рассмотрим первый случай: элементарный квадрат. Действительно, 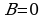 ,
, 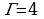 , получаем, что:
, получаем, что: 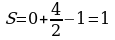 .
.
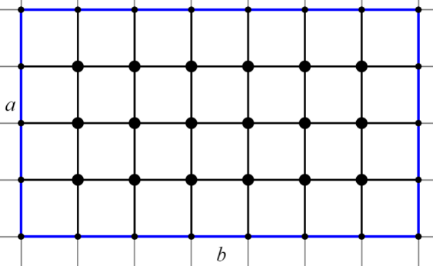 Далее рассмотрим произвольный прямоугольник со сторонами равными a и b. Для начала подсчитаем количество внутренних узлов, для этого обозначим их. Для удобства счёта, перенесём все внутренние узлы, в центры квадратов, для которых любой внутренний узел является верхней левой вершиной.
Далее рассмотрим произвольный прямоугольник со сторонами равными a и b. Для начала подсчитаем количество внутренних узлов, для этого обозначим их. Для удобства счёта, перенесём все внутренние узлы, в центры квадратов, для которых любой внутренний узел является верхней левой вершиной.
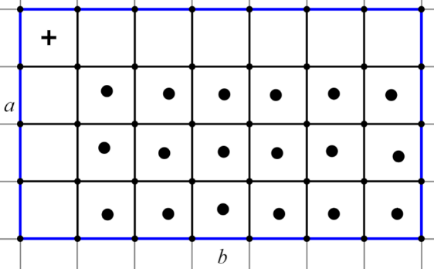 Теперь можем заметить, что счёт узлов, свёлся к счёту квадратов с узлом внутри. Для этого нам необходимо вычесть столбец и строку, которые не содержат узлы внутри себя. При вычитании строки и столбца мы вычли левую верхнюю клетку (клетка с крестиком) два раза, значит, нам нужно вернуть её один раз. Получаем, что количество внутренних узлов равно:
Теперь можем заметить, что счёт узлов, свёлся к счёту квадратов с узлом внутри. Для этого нам необходимо вычесть столбец и строку, которые не содержат узлы внутри себя. При вычитании строки и столбца мы вычли левую верхнюю клетку (клетка с крестиком) два раза, значит, нам нужно вернуть её один раз. Получаем, что количество внутренних узлов равно: 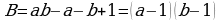 .
.
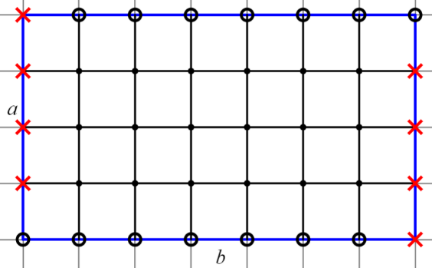 Количество граничных узлов можем посчитать следующим образом. На каждой стороне нашего прямоугольника начиная с верхнего левого узла отметим число узлов, равное длине стороны, в нашем случае
Количество граничных узлов можем посчитать следующим образом. На каждой стороне нашего прямоугольника начиная с верхнего левого узла отметим число узлов, равное длине стороны, в нашем случае 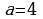 , а
, а 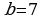 . Получаем, что
. Получаем, что 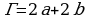 .
.
Подставляем полученные данные в формулу: 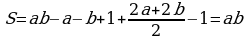 .
.
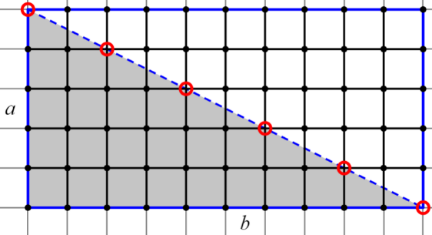 Далее рассмотрим случай для прямоугольного треугольника, получаемого путём разделения прямоугольника любой из своих диагоналей.
Далее рассмотрим случай для прямоугольного треугольника, получаемого путём разделения прямоугольника любой из своих диагоналей.
Разделим наш прямоугольник на два прямоугольных треугольника любой из диагоналей. И посчитаем внутренние узлы.
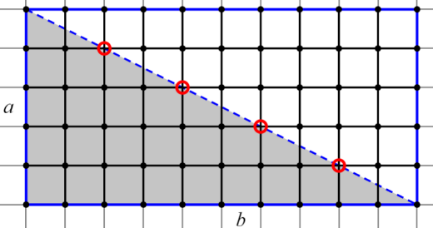 Для начала из прямоугольника уберём все узлы, которые лежат на диагонали, т.к. они являются граничными узлами полученного треугольника. Но убрав все узлы диагонали, мы также убрали узлы, которые являются вершинами треугольника, значит, нам нужно их вернуть. Таким образом получаем, что количество внутренних узлов в прямоугольнике стало равно
Для начала из прямоугольника уберём все узлы, которые лежат на диагонали, т.к. они являются граничными узлами полученного треугольника. Но убрав все узлы диагонали, мы также убрали узлы, которые являются вершинами треугольника, значит, нам нужно их вернуть. Таким образом получаем, что количество внутренних узлов в прямоугольнике стало равно 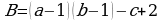 , где c - это количество узлов, лежащих на диагонали (вместе с вершинами прямоугольника!). Так как при разбиении прямоугольника получается два треугольника, то количество внутренних узлов необходимо поделить на два:
, где c - это количество узлов, лежащих на диагонали (вместе с вершинами прямоугольника!). Так как при разбиении прямоугольника получается два треугольника, то количество внутренних узлов необходимо поделить на два: 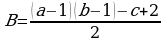 .
.
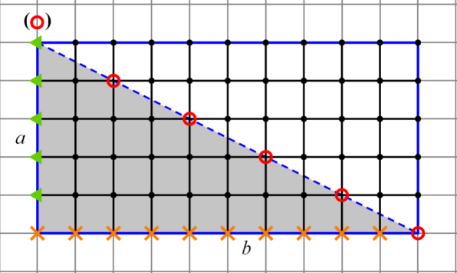 Посчитаем граничные узлы. Для этого рассмотрим треугольник и на каждой стороне обозначим такое число узлов, скольким равна длина стороны. В данном случае
Посчитаем граничные узлы. Для этого рассмотрим треугольник и на каждой стороне обозначим такое число узлов, скольким равна длина стороны. В данном случае 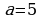 ,
, 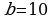 ,
, 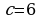 . Если мы начнём обозначать узлы с верхней левой вершины, то обойдя весь треугольник мы увидим, что верхнюю левую вершину мы переобозначили два раза, значит, нам необходимо вычесть одно переобозначение. Получаем, что количество граничных узлов равно:
. Если мы начнём обозначать узлы с верхней левой вершины, то обойдя весь треугольник мы увидим, что верхнюю левую вершину мы переобозначили два раза, значит, нам необходимо вычесть одно переобозначение. Получаем, что количество граничных узлов равно: 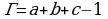 . Подставим:
. Подставим: 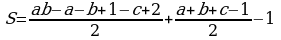 или
или 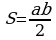 .
.
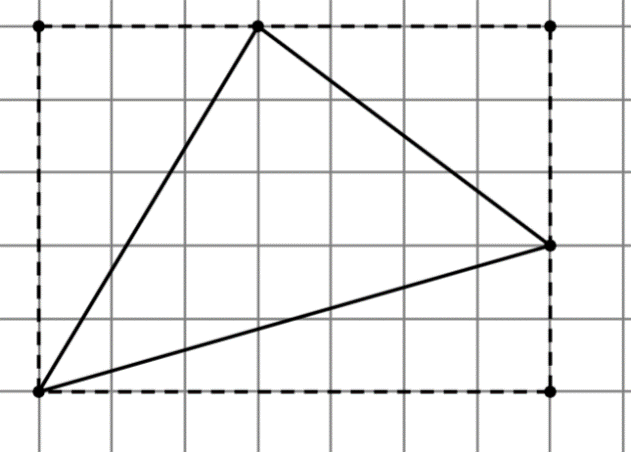 Далее рассмотрим произвольный треугольник. Его площадь можно найти путём вычитания из прямоугольника прямоугольных треугольников. А так как мы доказали справедливость формулы Пика для прямоугольника и прямоугольного треугольника, то формула будет верна и для произвольного треугольника в силу триангуляции (любой треугольник можно разбить на два прямоугольных).
Далее рассмотрим произвольный треугольник. Его площадь можно найти путём вычитания из прямоугольника прямоугольных треугольников. А так как мы доказали справедливость формулы Пика для прямоугольника и прямоугольного треугольника, то формула будет верна и для произвольного треугольника в силу триангуляции (любой треугольник можно разбить на два прямоугольных).
1.6. Исключения
Далее стоит отметить важные замечания.
Формула применима не для всех фигур, изображённых на клетчатой бумаге. Покажем все случаи.
| 1. Формула Пика не применима для многоугольников, которые содержат «дыру» внутри себя. 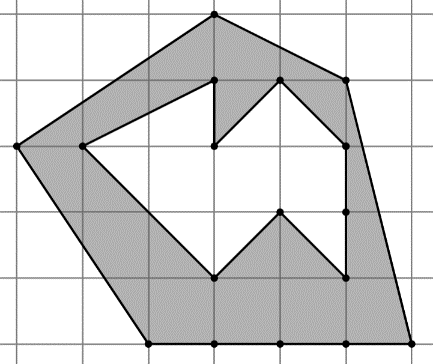
| 2. Формула Пика не применима для фигур, которые имеют точки самопересечения. 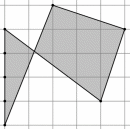
|
| 3. Формула Пика не применима для фигур, граничные линии которых имеют форму дуг окружностей. 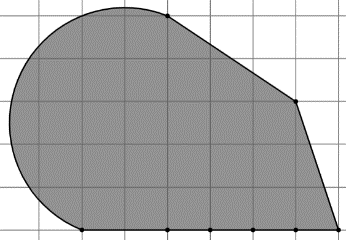
| 4. Формула Пика не применима для фигур, вершины которых находятся не в узловых точках. 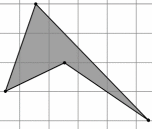
|
Также стоит отметить, что после усовершенствования формулы, она начинает работать, но данный случай не рассматривается нами в данной работе и будет рассмотрен в дальнейшем.
Глава 2. Задачи
2.1. Решение типовых задач
Продемонстрируем решение типовых задач через формулы планиметрии и формулу Пика для сравнения сложности требуемых вычислений.
Задание: найдите площадь многоугольника, зная, что длина стороны квадрата равна 1.
| Чертёж | Вычисление формулами планиметрии | Вычисление формулой Пика |
| 
| 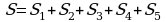 ; ;
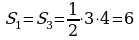 ; ;
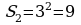 ; ;
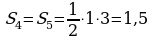 ; ;
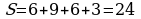 . .
| 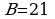 ; ;
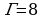 ; ;
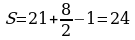 . .
|
| 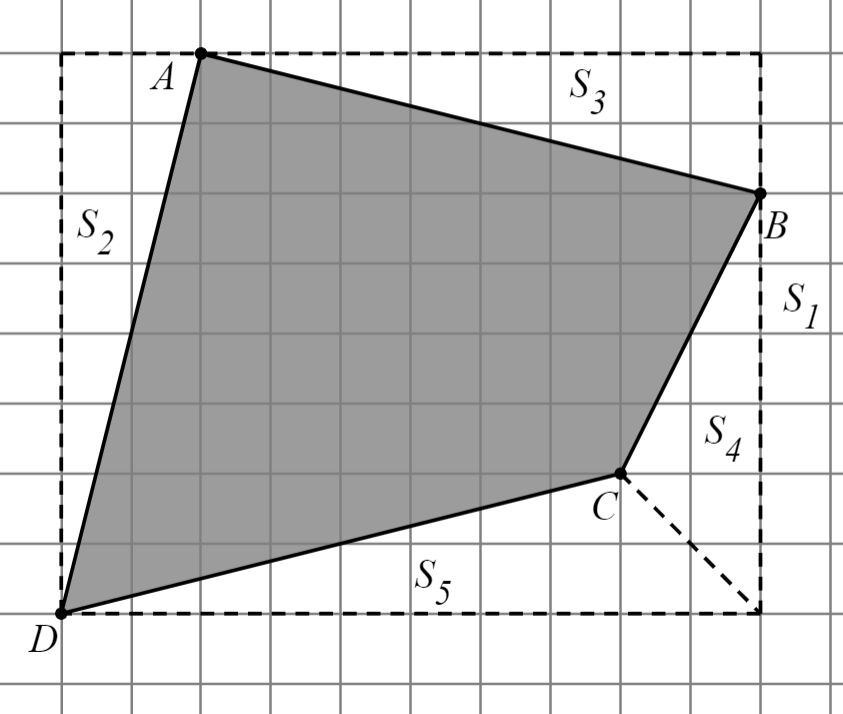
|  ; ;
 ; ;
 ; ;
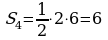 ; ;
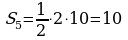 ; ;
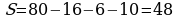 . .
| 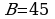 ; ;
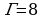 ; ;
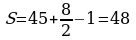 . .
|
| 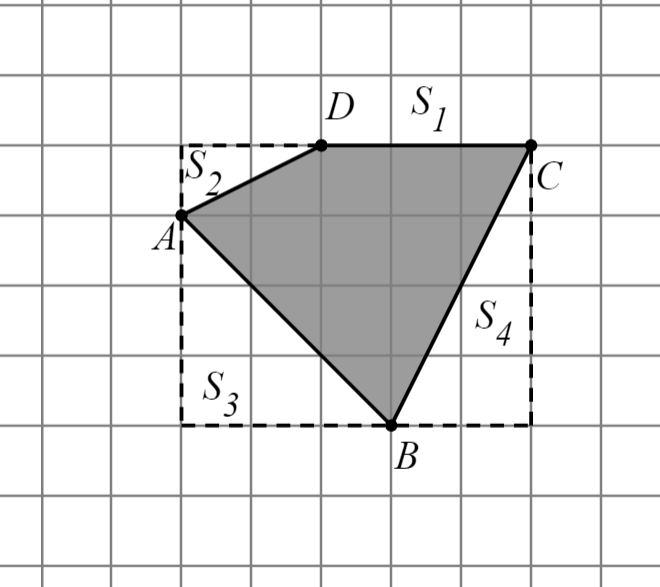
| 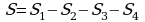 ; ;
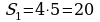 ; ;
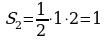 ; ;
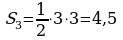 ; ;
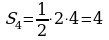 ; ;
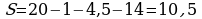 . .
| 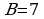 ; ;
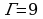 ; ;
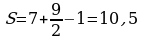 . .
|
| 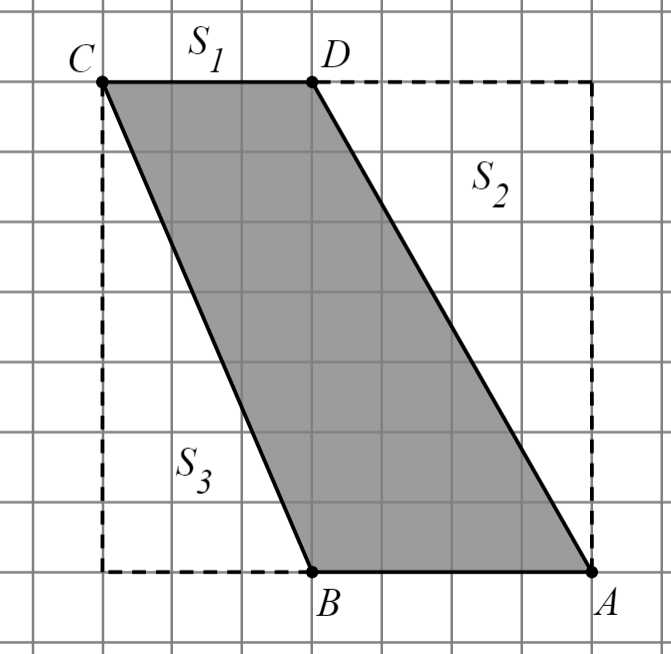
|  ; ;
 ; ;
 ; ;
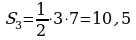 ; ;
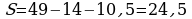 . .
| 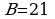 ; ;
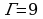 ; ;
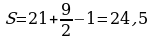 . .
|
| 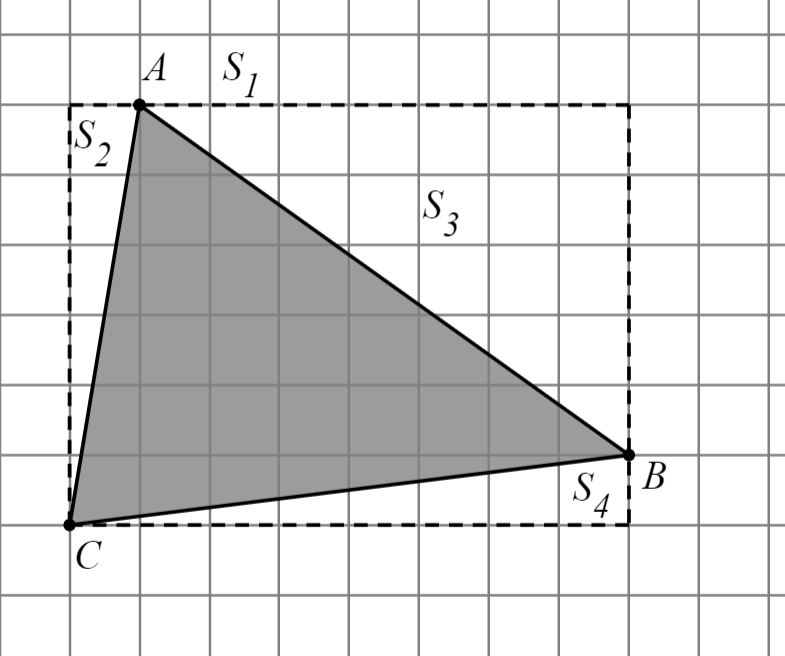
| 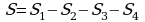 ; ;
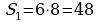 ; ;
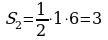 ; ;
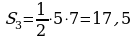 ; ;
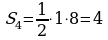 ; ;
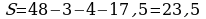 . .
| 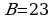 ; ;
 ; ;
 . .
|
| 
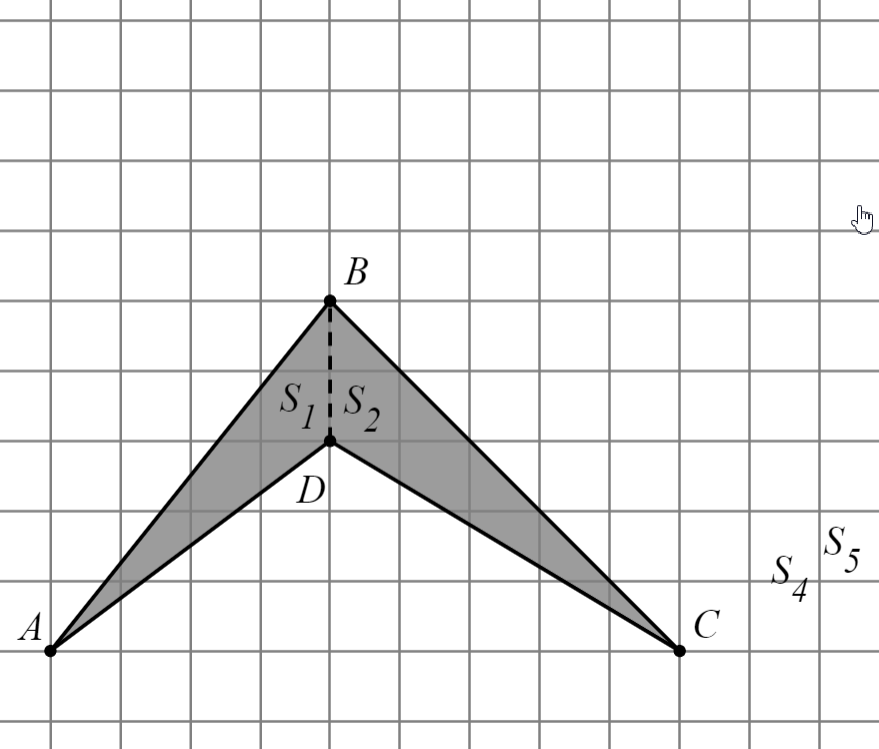
| 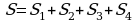 ; ;
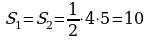 ; ;
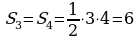 ; ;
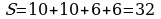 . .
| 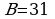 ; ;
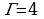 ; ;
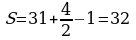 . .
|
| 
| 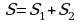 ; ;
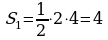 ; ;
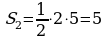 ; ;
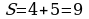 . .
| 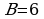 ; ;
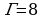 ; ;
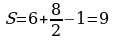 . .
|
2.2. Сборник задач
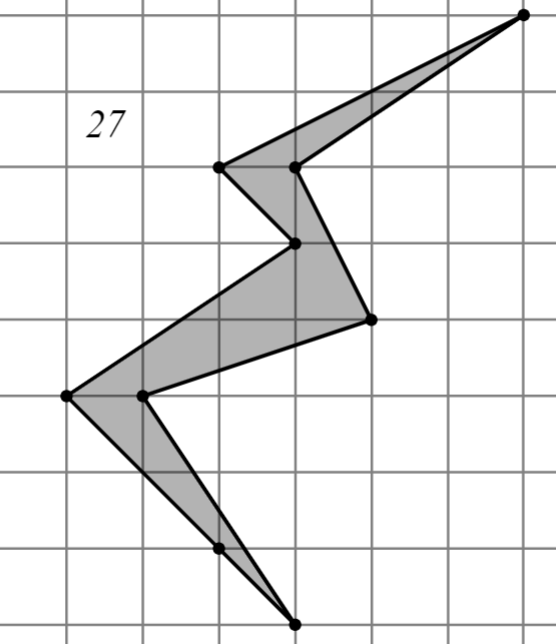
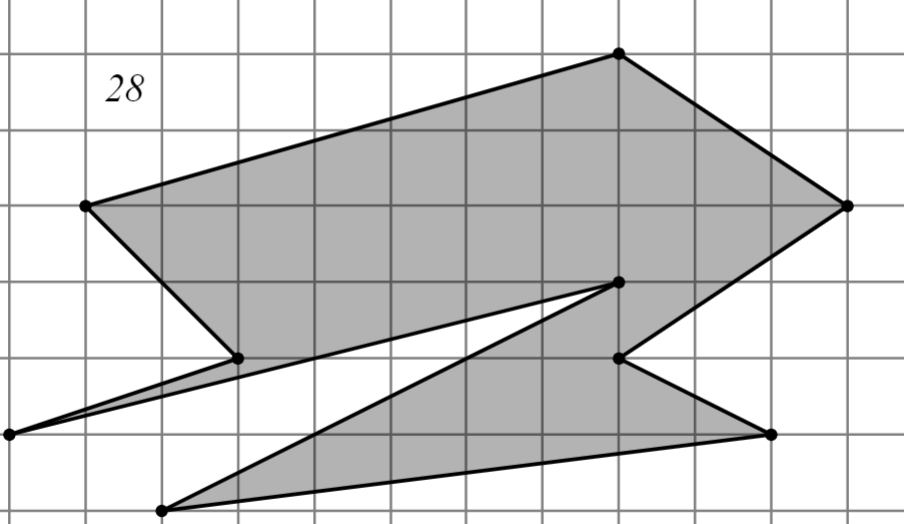
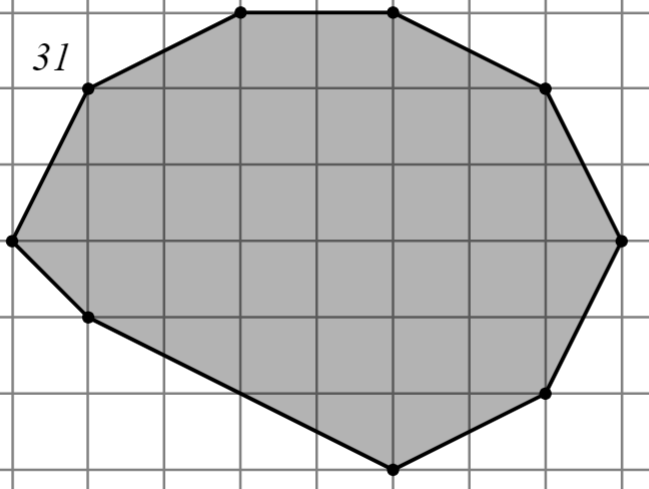
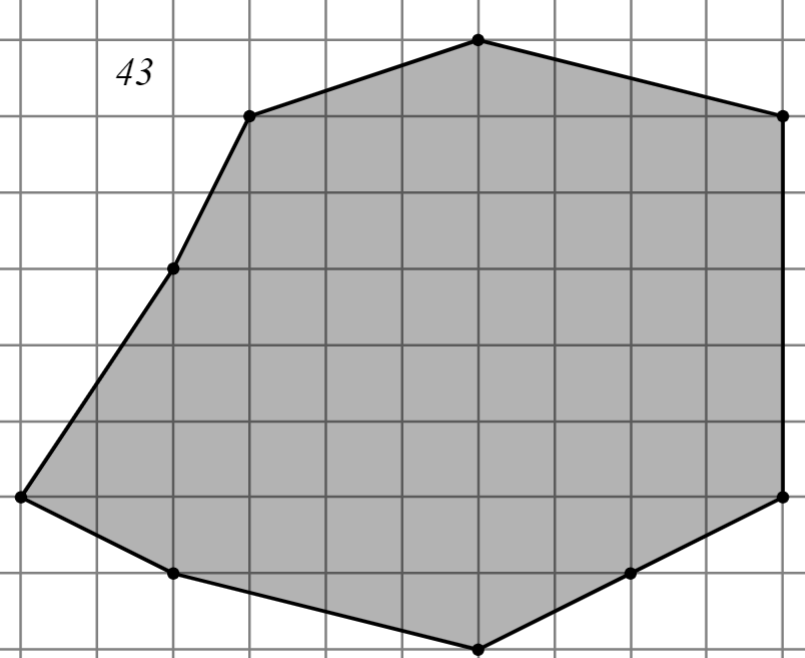
2.2.1. Первый уровень
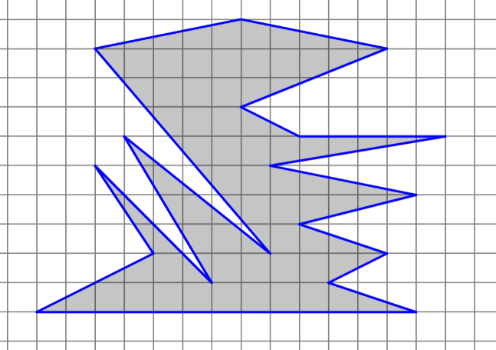
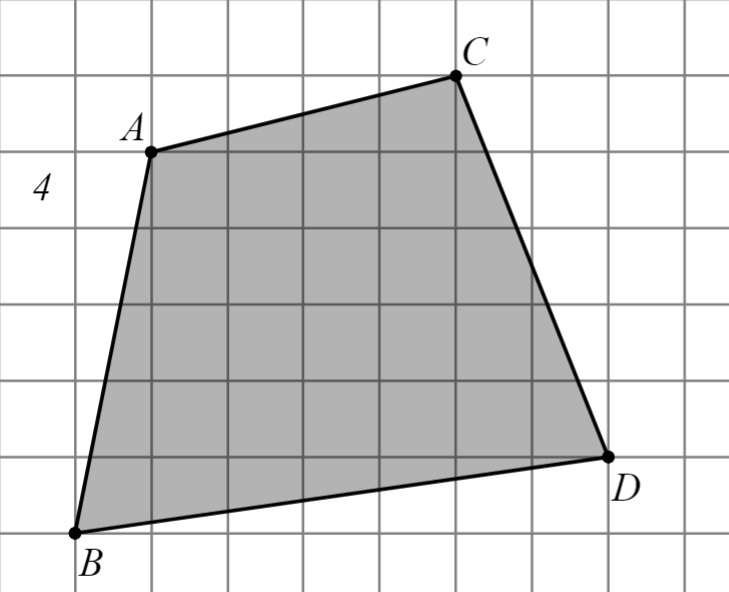
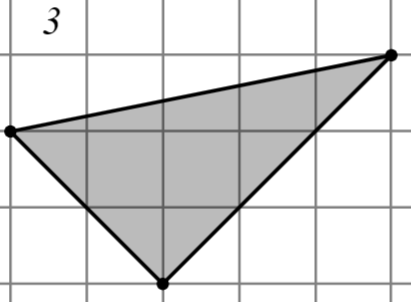
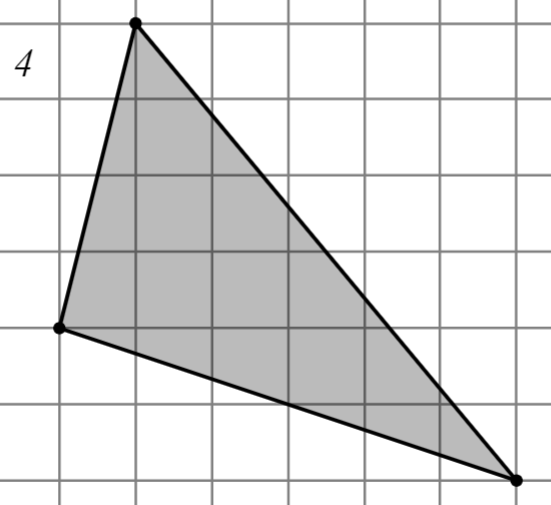
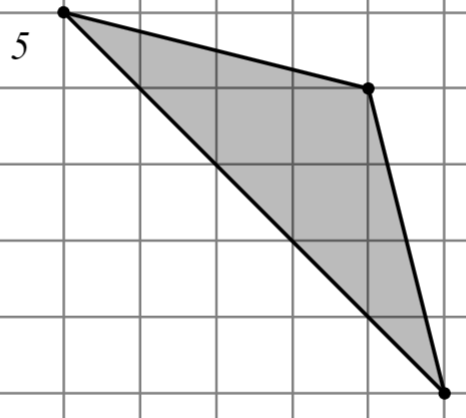
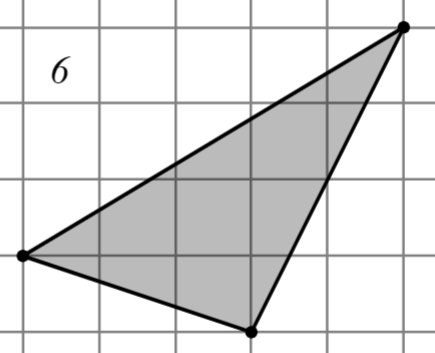
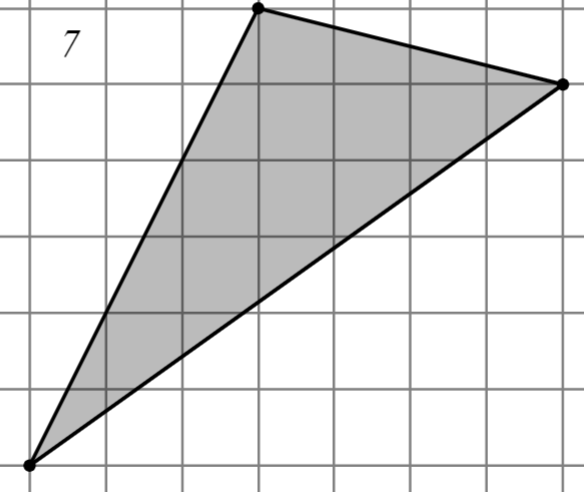
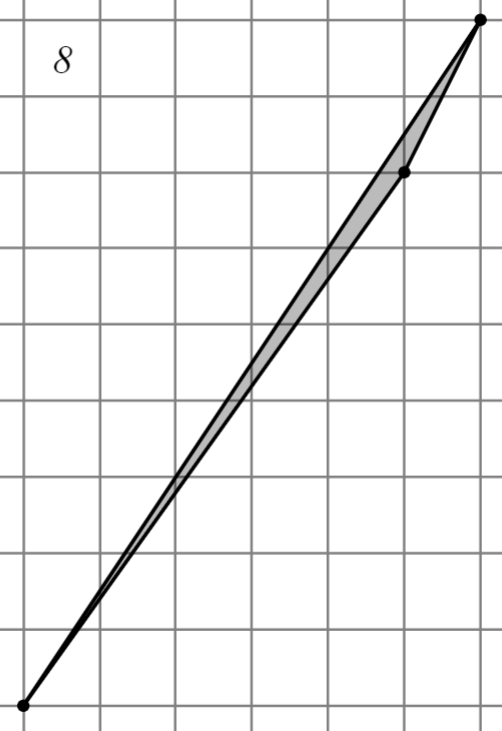
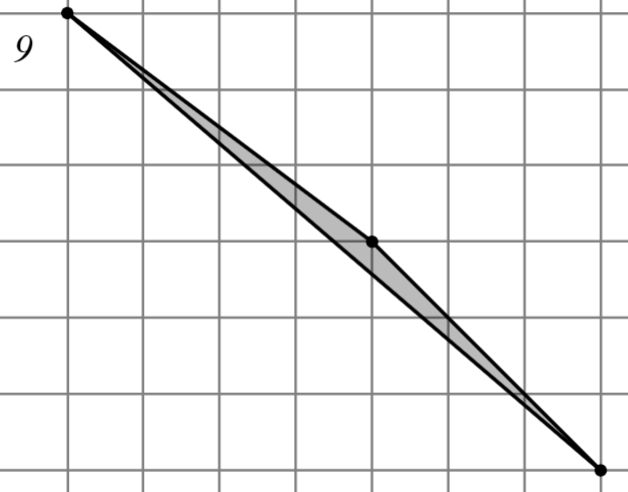
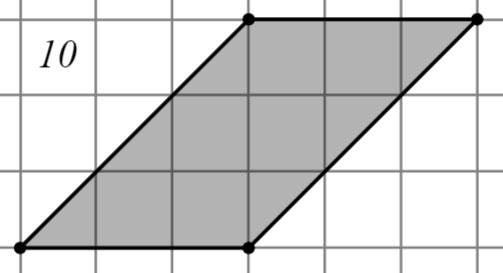
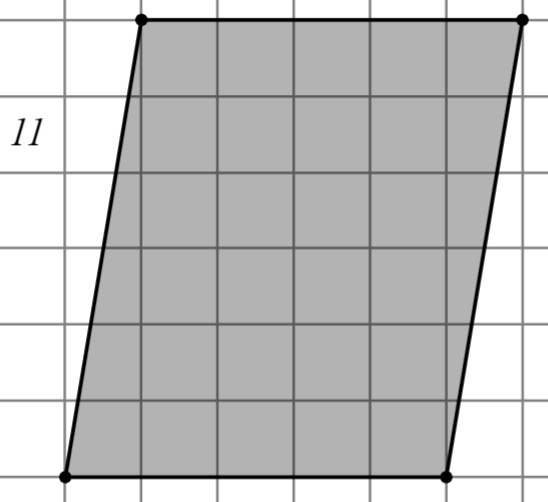
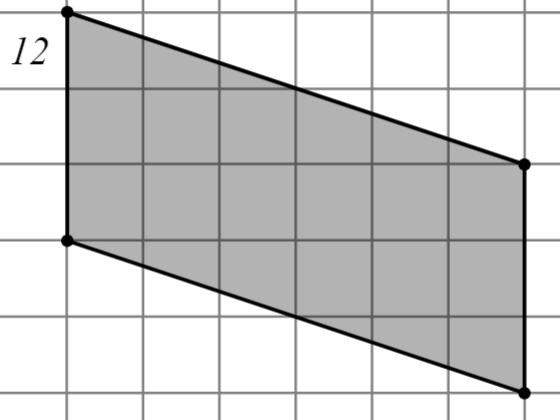
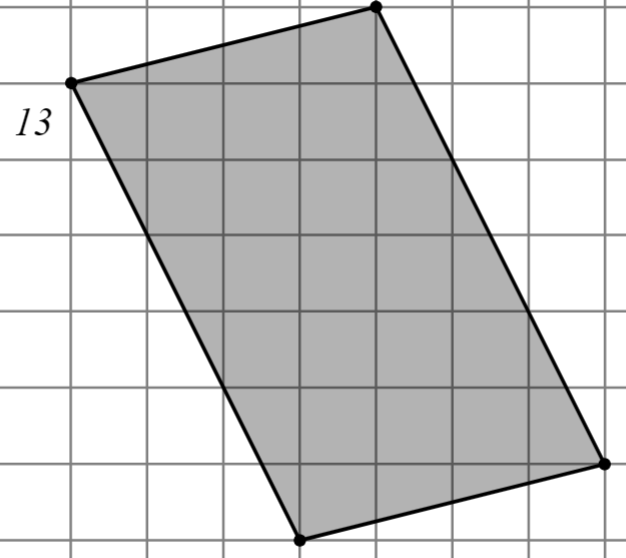
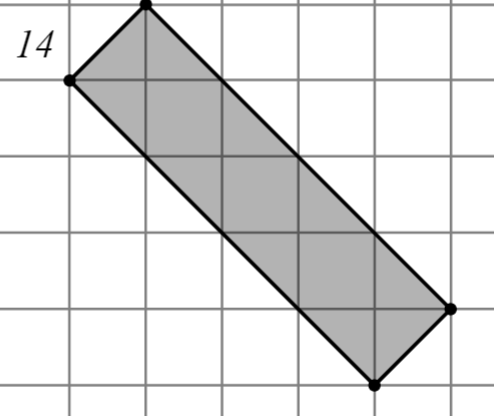
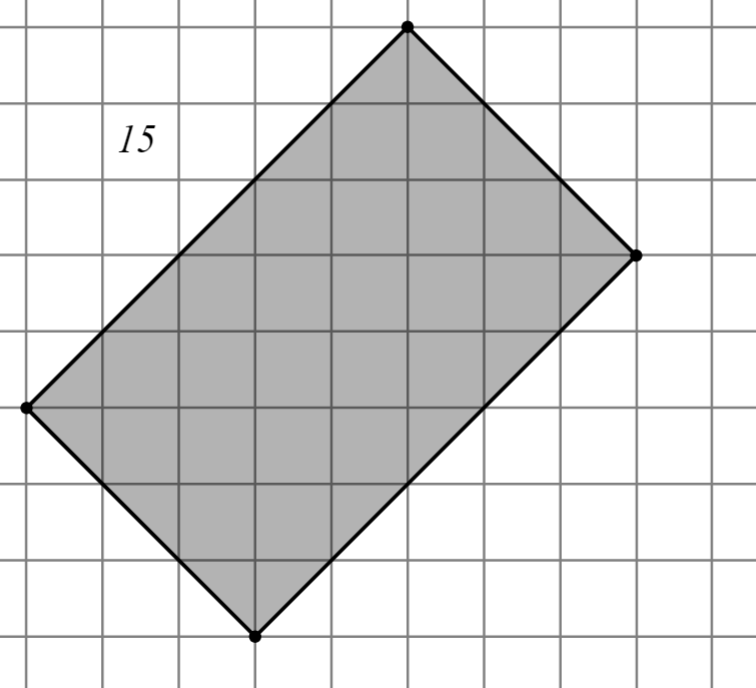
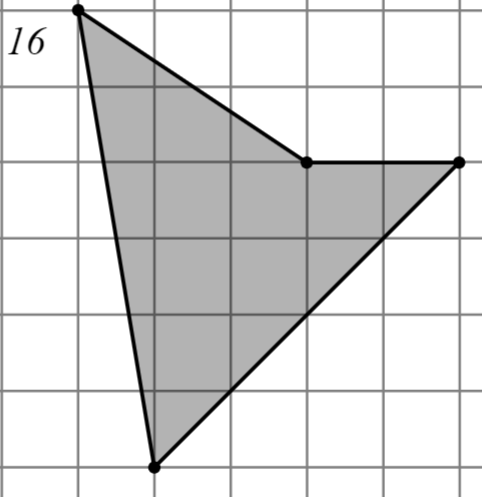
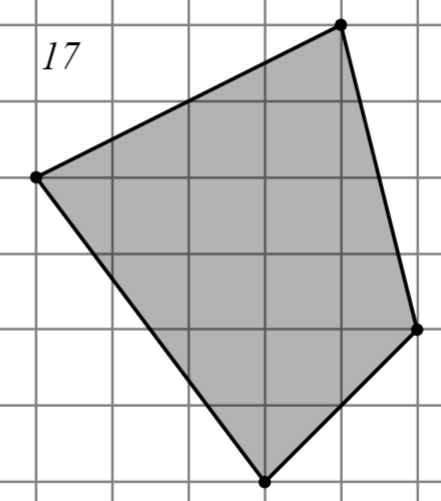
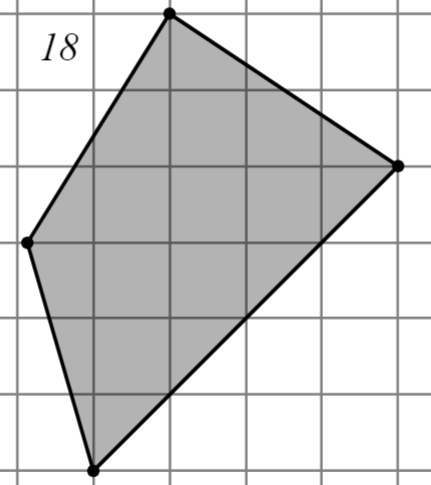
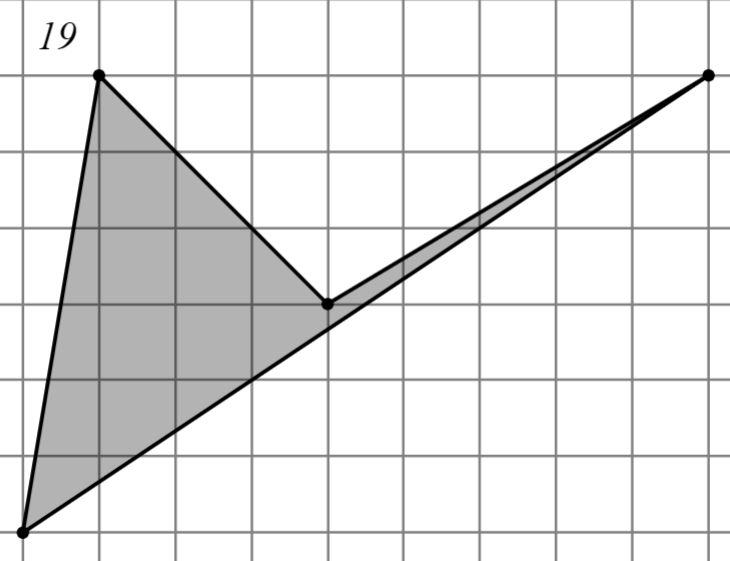
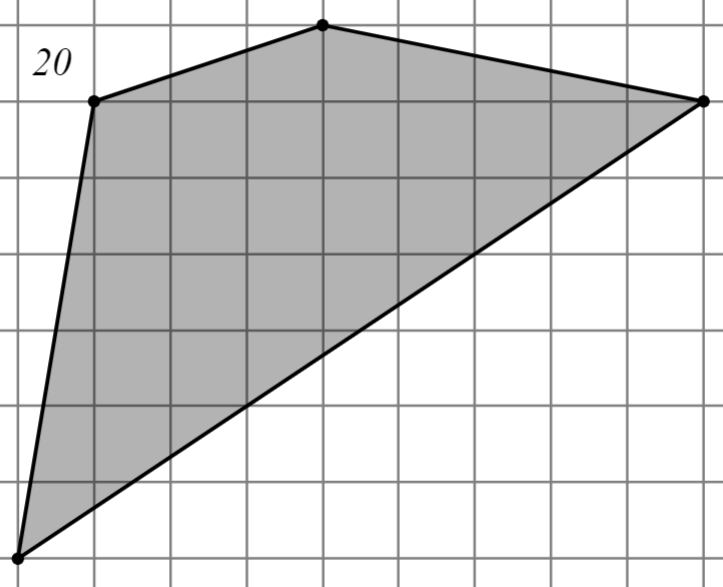
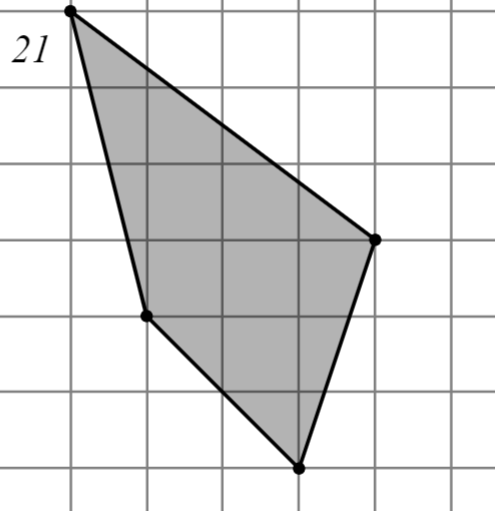
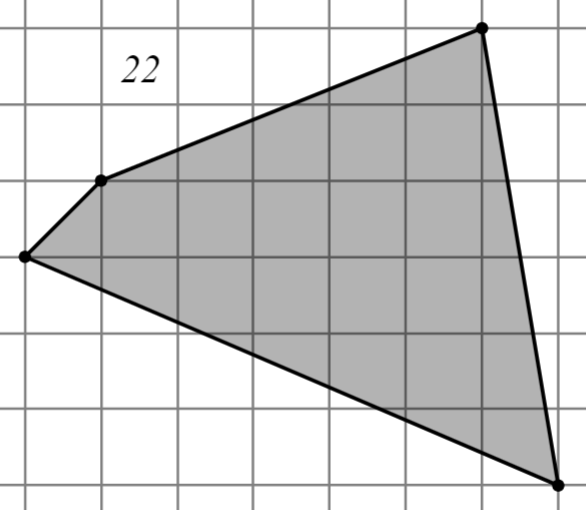
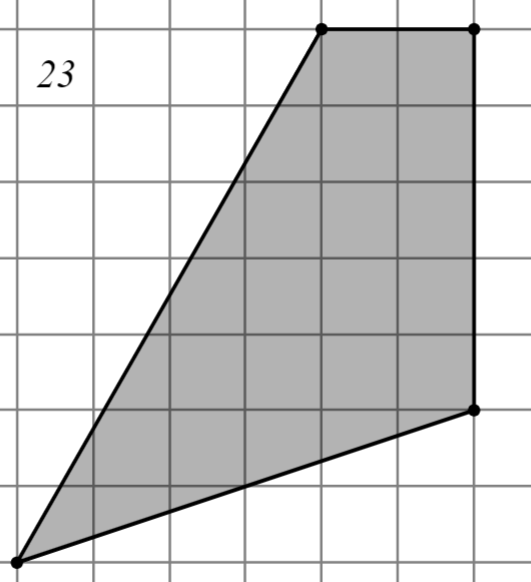
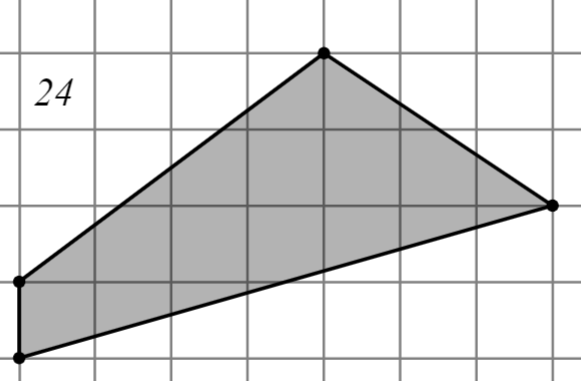
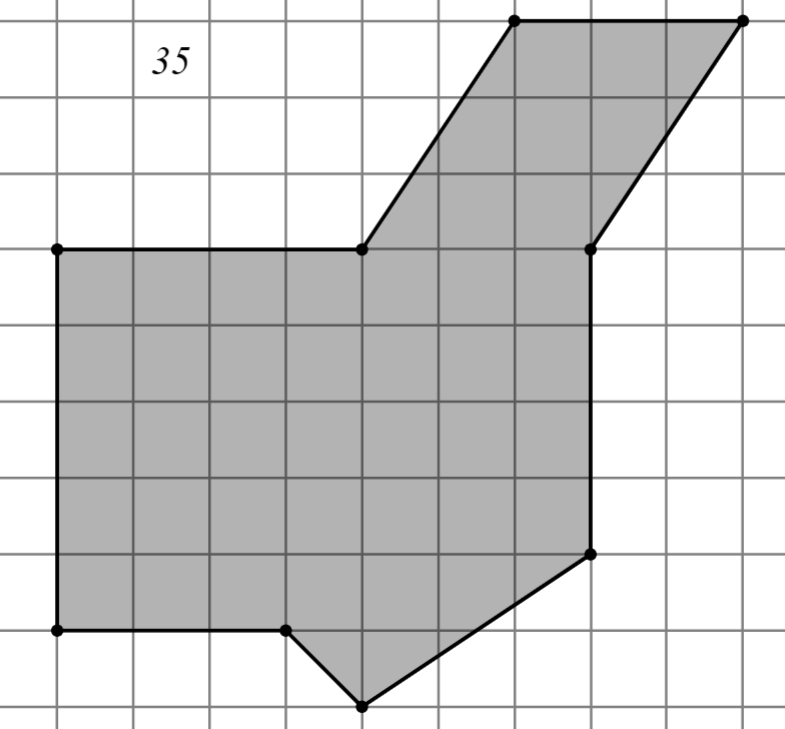
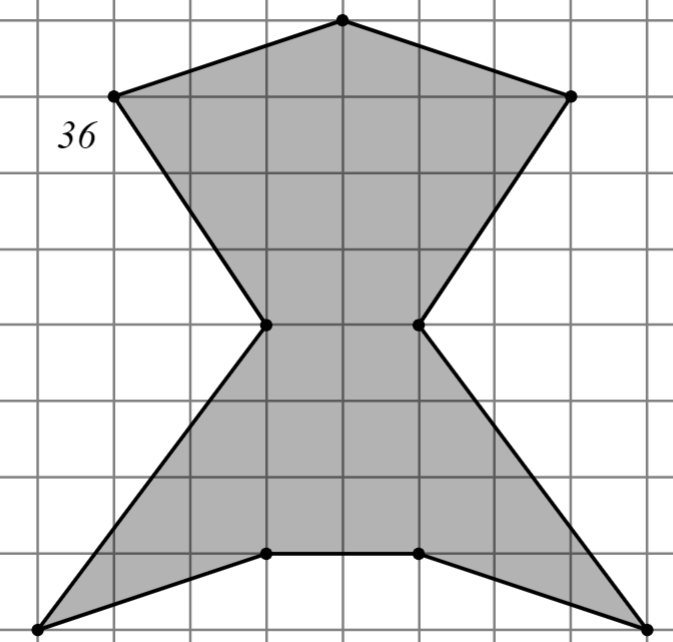
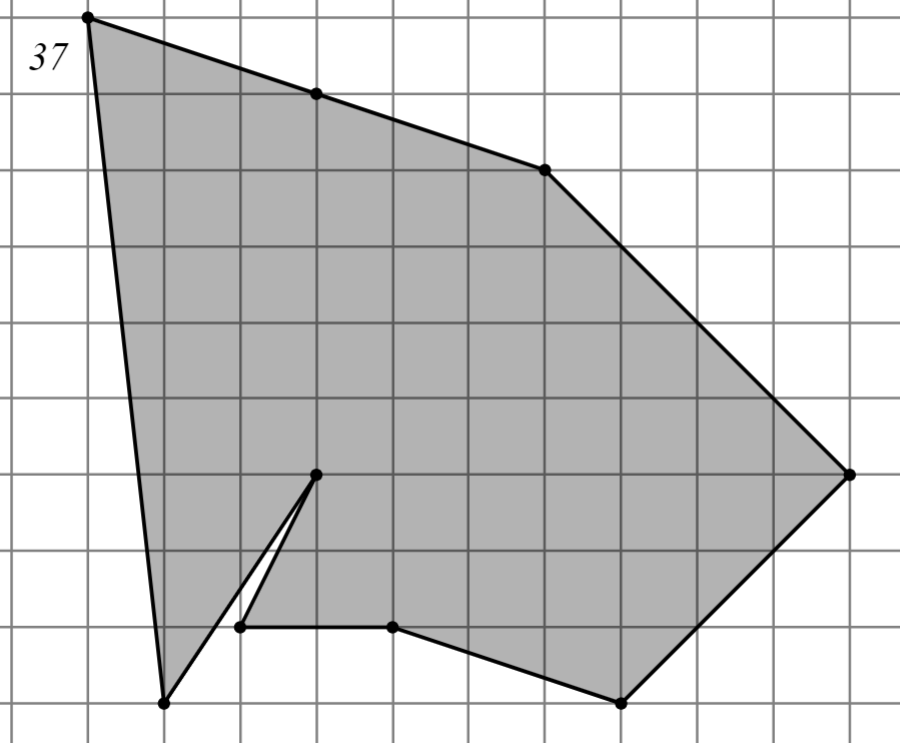
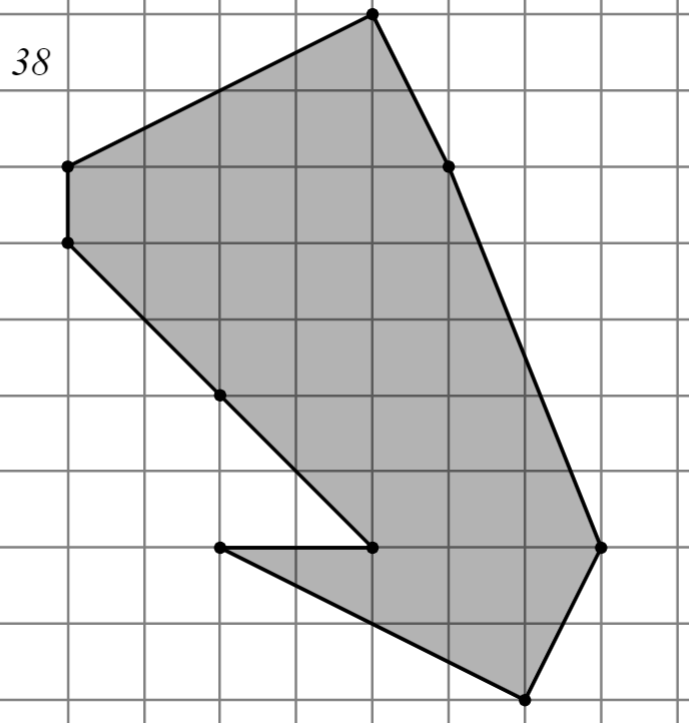
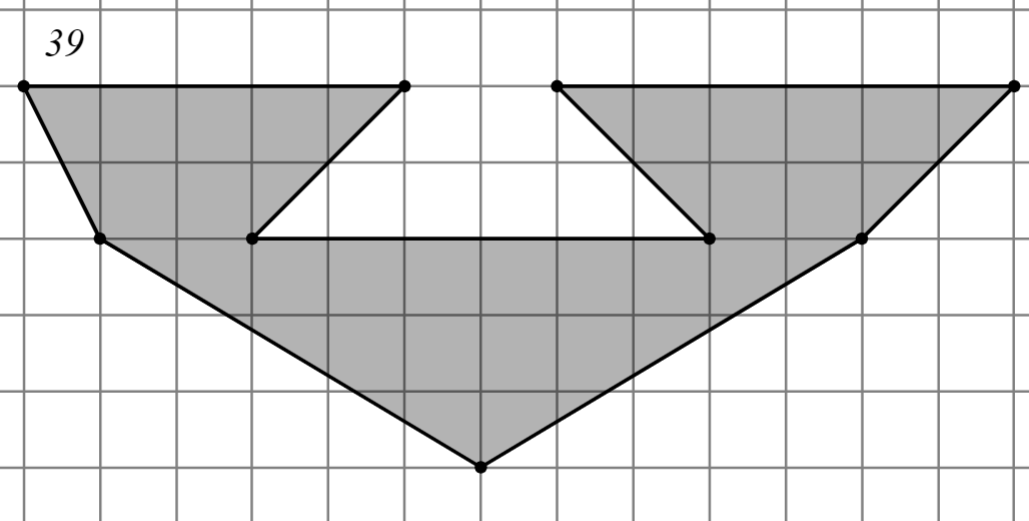
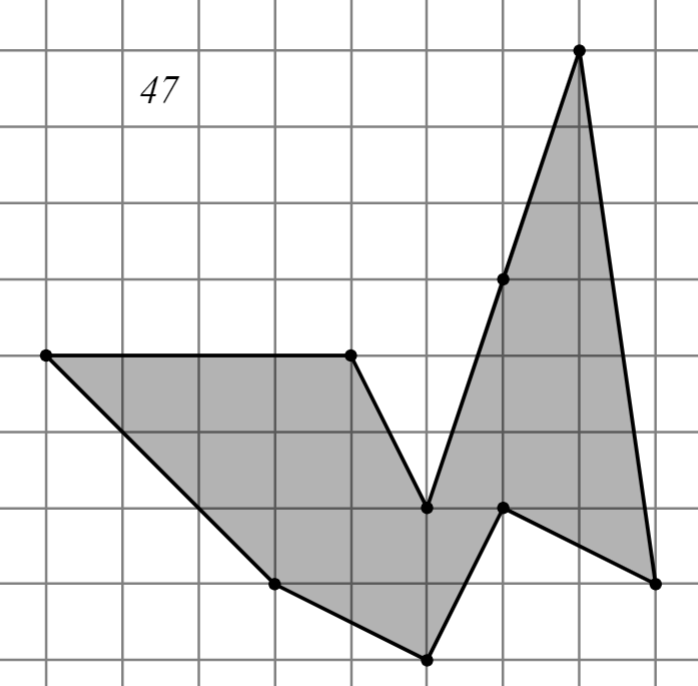
Задание: Найдите площадь многоугольника, изображённого на клетчатой бумаге, где длина квадрата равна 1.
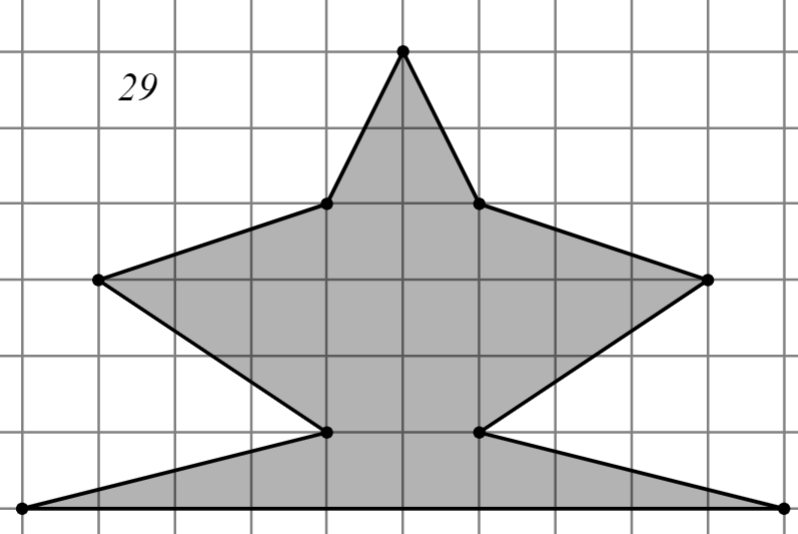
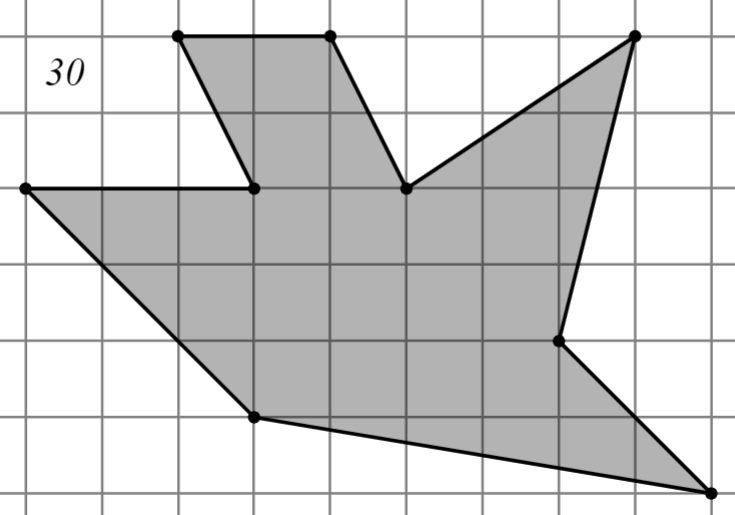
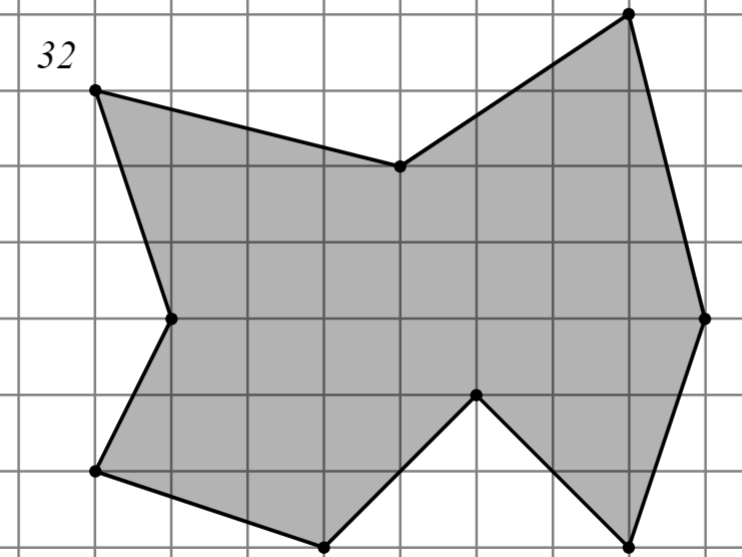
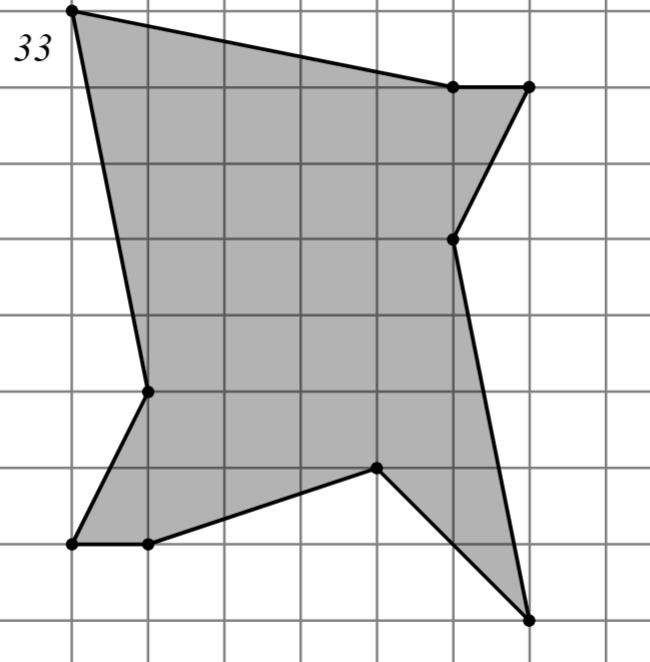
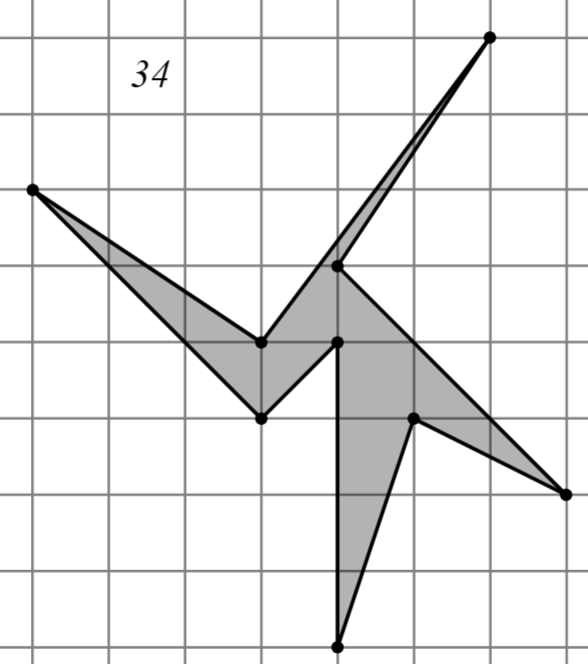
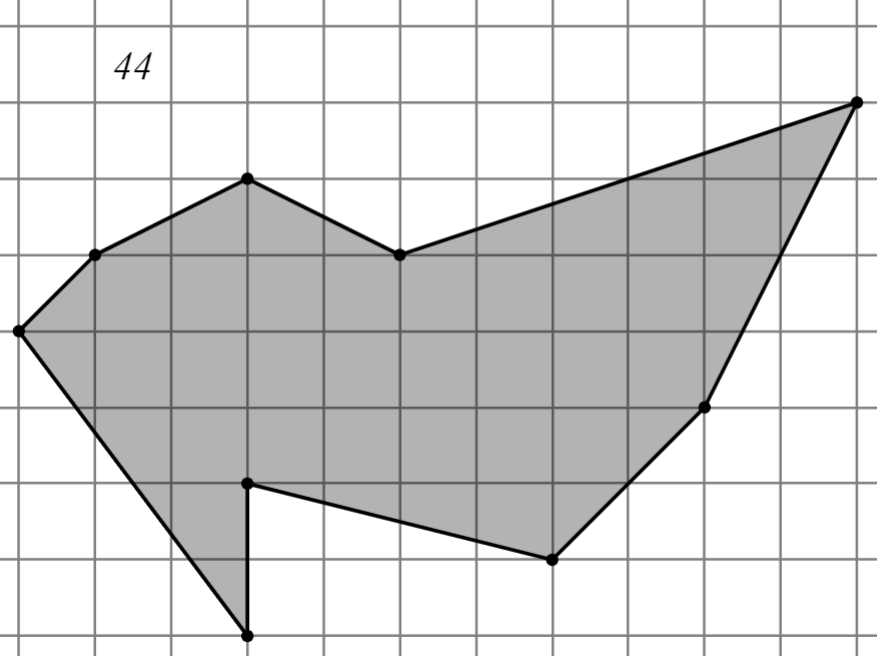
2.2.2. Второй уровень
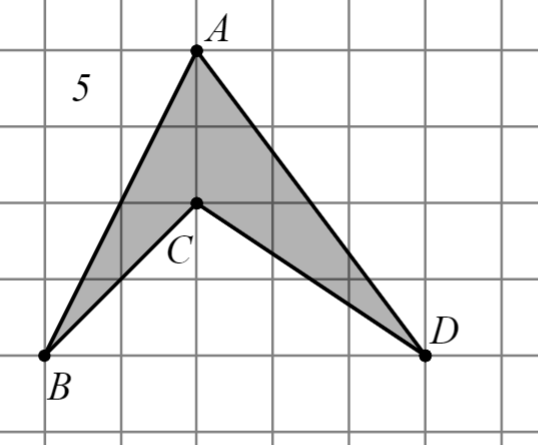
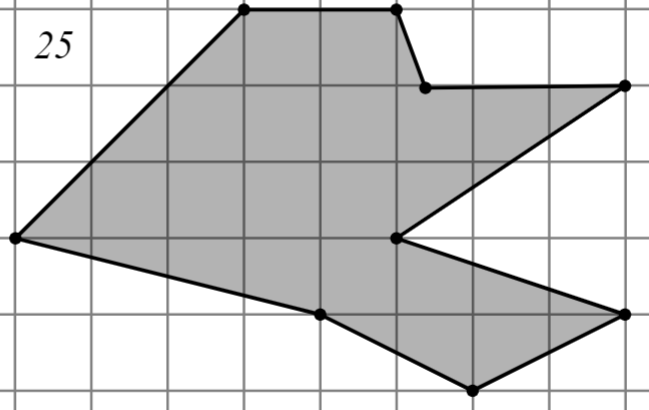
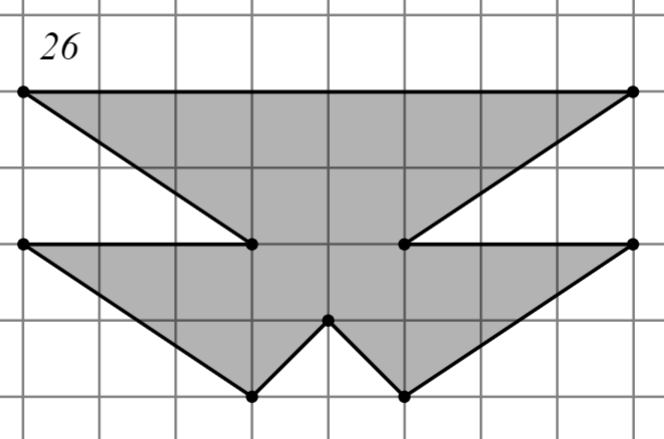
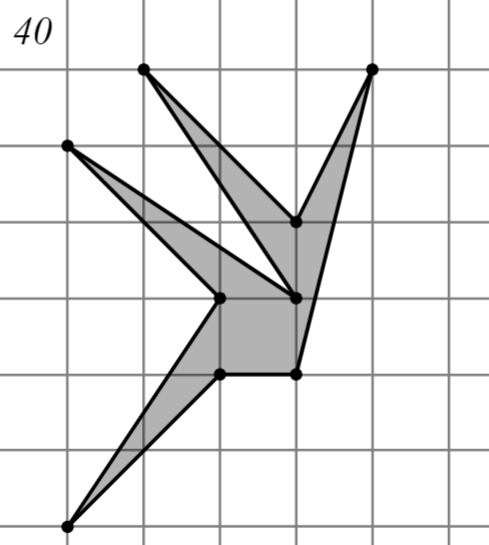
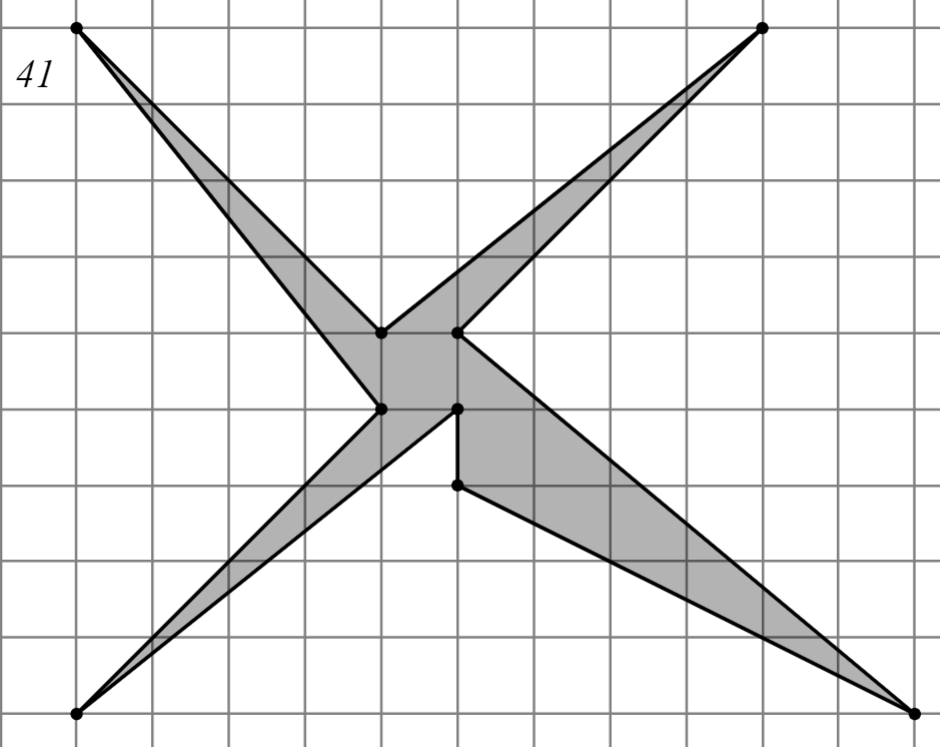
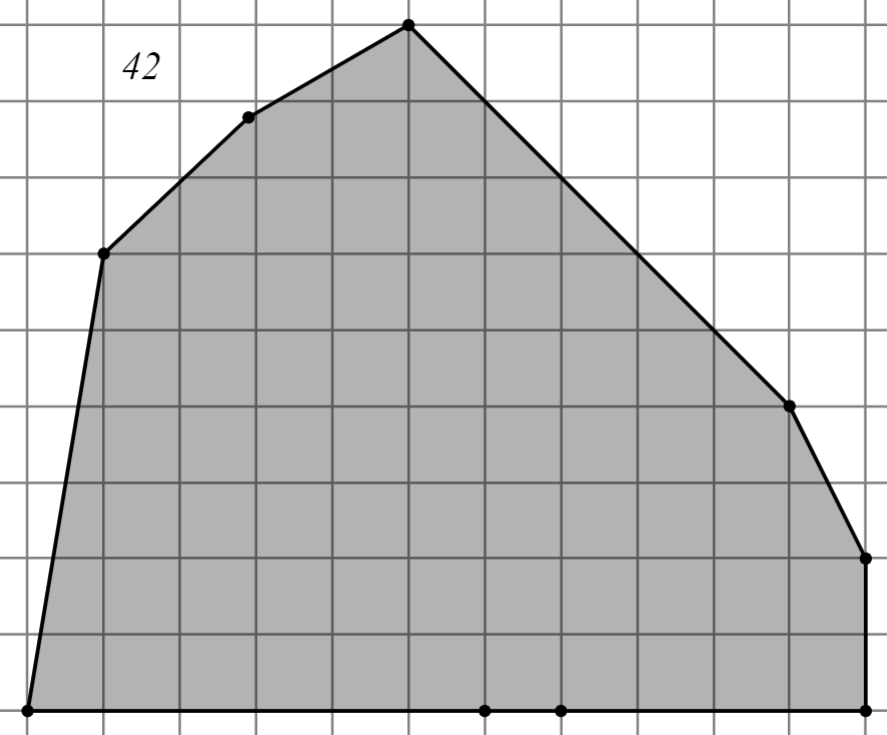
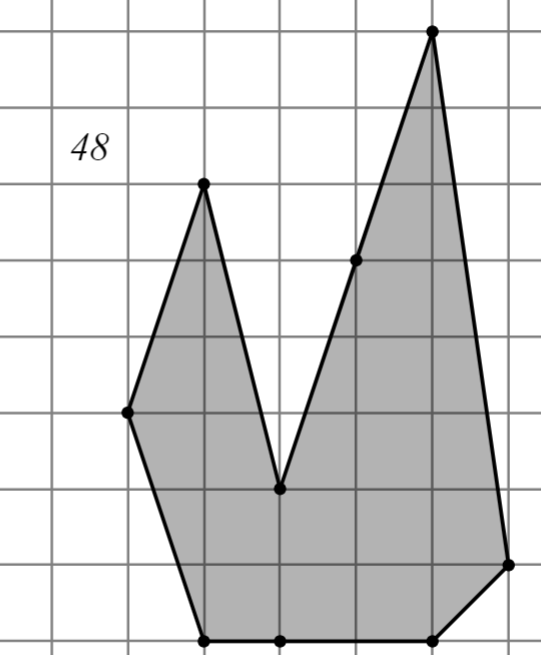
Задание: Найдите площадь многоугольника, изображённого на клетчатой бумаге, где длина квадрата равна 1.
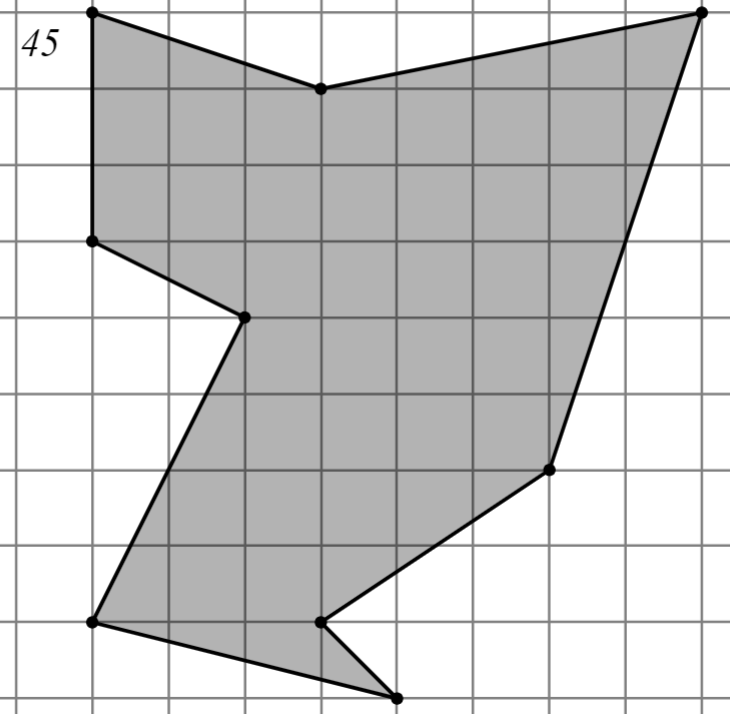
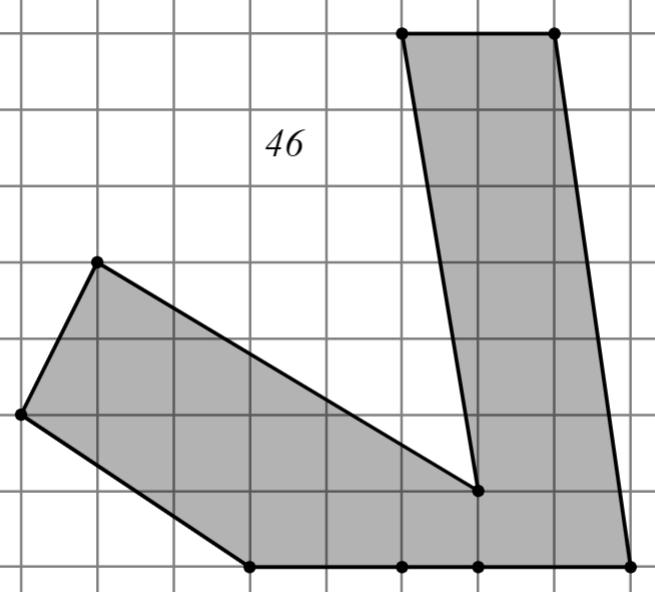
2.2.3. Третий уровень
Задание 1. Шахматный король обошел доску 88 клеток, побывав на каждом поле ровно 1 раз и последним ходом вернувшись на исходное поле. Ломаная, последовательно соединяющая центры полей, не имеет самопересечений.
а. нарисуйте такую ломаную;
б. найдите площадь, ограниченную этой ломаной.
Задание 2. Нарисуйте треугольник площади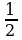 , у которого все стороны больше 5, а вершины лежат в узлах сетки.
, у которого все стороны больше 5, а вершины лежат в узлах сетки.
Задание 3. Замкнутая не самопересекающаяся ломаная идет по линиям сетки и проходит по одному разу через все узлы клетчатого квадрата 77. Найдите площадь фигуры, ограниченной этой ломаной.
Задание 4. Пусть А и В – два узла клетчатой бумаги, из которых второй на p клеток правее и на q клеток выше первого. Чему равно расстояние от прямой АВ до ближайшего к ней узла, не лежащего на этой прямой?
Задание 5. Найдется ли правильный треугольник с вершинами в узлах сетки?
Задание 6. Найдется ли прямоугольный треугольник с целыми сторонами и вершинами в узлах сетки
а. на сторонах которого нет узлов сетки кроме вершин;
б. ни одна из сторон которого не проходит по линиям сетки?
Задание 7. Докажите формулу Пика, разбив доказательство на ряд шагов:
а. проверьте формулу Пика для прямоугольника со сторонами, идущими по линиям сетки;
б. докажите формулу Пика для многоугольника со сторонами, идущими по линиям сетки;
в. докажите формулу Пика для прямоугольного треугольника с катетами, идущими по линиям сетки;
г. докажите формулу Пика для многоугольника, составленного из двух многоугольников, для которых формула Пика уже доказана;
д. пусть многоугольник, для которого формула Пика уже проверена, составлен из двух многоугольников. Докажите, что если формула Пика выполняется для одного из них, то она выполняется и для другого;
е. докажите формулу Пика для произвольного треугольника с вершинами в узлах сетки;
ё. докажите, что всякий выпуклый многоугольник можно разбить диагоналями на треугольники;
ж. докажите, что любой (не обязательно выпуклый) многоугольник можно разбить диагоналями на треугольники;
з. докажите формулу Пика для произвольного многоугольника с вершинами в узлах сетки.
Задание 8. Точку M внутри треугольника соединили с его вершинами, в результате треугольник разбился на три равновеликие части. Докажите, что M – точка пересечения медиан треугольника.
Задание 9. Вершины треугольника расположены в узлах клетчатой бумаги, причем на его сторонах других узлов нет, а внутри есть ровно один узел О. Докажите, что О – точка пересечения медиан треугольника.
Задание 10. Докажите, что найдется прямая, проходящая через два узла клетчатой бумаги, и не лежащий на этой прямой узел, такой, что расстояние между ними меньше 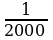 .
.
Задание 11. Докажите, что для любого многоугольника с вершинами в узлах сетки отношение его площади к квадрату любой стороны рационально.
Задание 12. Докажите, что если вершины выпуклого n-угольника лежат в узлах клетчатой бумаги, а внутри и на его сторонах других узлов нет, то n 5.
Задание 13. На большой шахматной доске отметили 2n клеток так, что ладья может ходить по всем отмеченным клеткам, не перепрыгивая через неотмеченные. Докажите, что фигуру из отмеченных клеток можно разрезать на n прямоугольников.
Задание 14. Ладья, шагая по одной клетке, за 64 хода обошла все клетки шахматной доски и вернулась на исходную клетку. Докажите, что число ходов по вертикали не равно числу ходов по горизонтали.
2.3. Проверочная работа
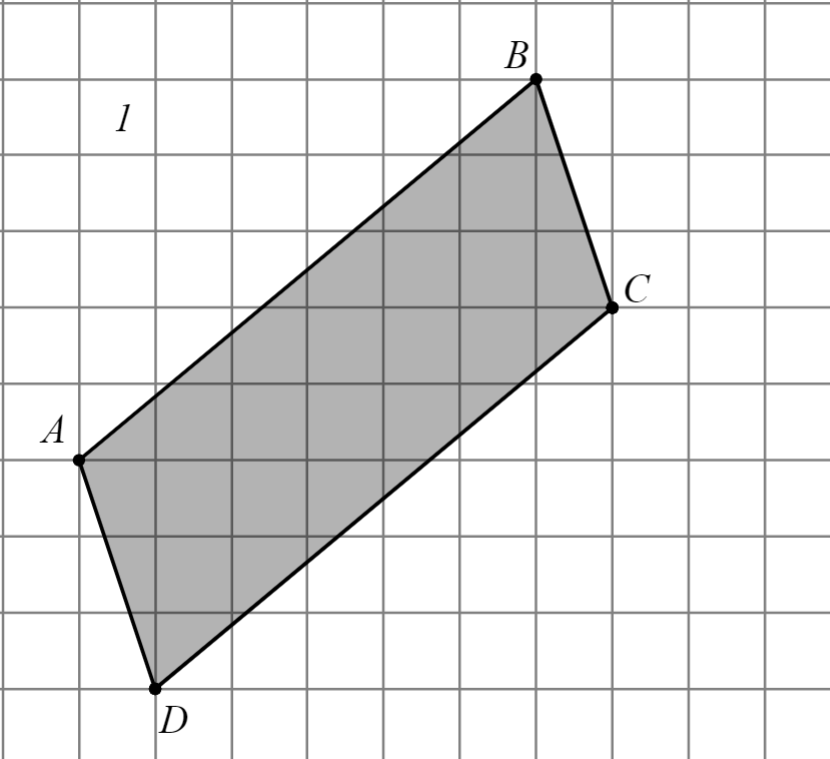
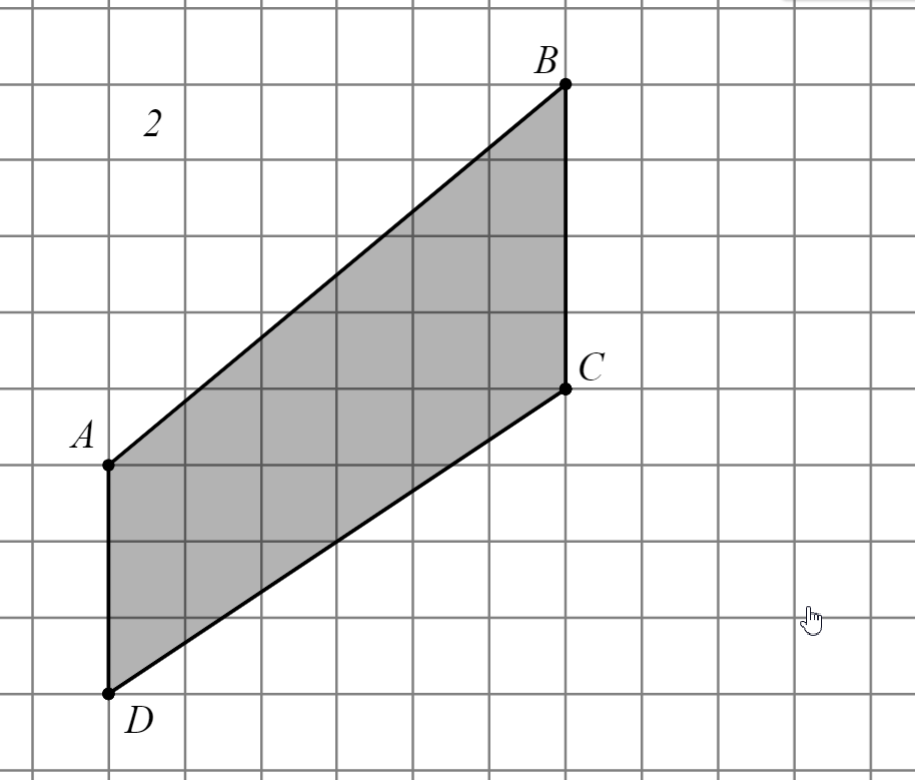
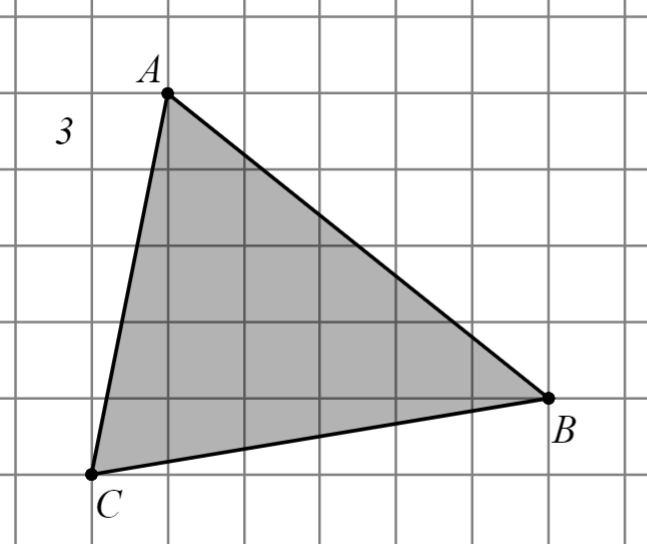
| Задание | Решение формулами планиметрии | Решение по формуле Пика |
| 
|
|
|
| 
|
|
|
| 
|
|
|
| 
|
|
|
| 
|
|
|
Заключение
В любом деле важную роль играет усердие, с которым выполняется та или иная работа. Настрой именно самого человека постичь новые знания и научиться новому. Как гласит одна из истин: «Хочешь научиться решать задачи, решай их». Именно желание и усердие самого человека могут подтолкнуть его на покорение новых вершин.
Данный сборник задач хоть и не претендует на право называться учебным пособием, но может быть существенным подспорьем в подготовке к общему государственному экзамену и кружковым занятиям по математике.
Список литературы
1. Вавилов В.В., Устинов А.В. Многоугольники на решётках. – М.: МЦНМО, 2006. – 72 с.: ил. ISBN 5-94057-246-4.
2. Геометрия на клетчатой бумаге. Малый МЕХмат МГУ. Режим доступа: Геометрия на клетчатой бумаге | 9-11 классы | Кружки | Малый мехмат МГУ (msu.ru)
3. Игнатьев Е.И. В царстве смекалки/Текстологическая обработка Ю.В. Нестеренко ; Под ред. М.К. Потапова. – 5-е изд., исправленное.- М.: Наука. Гл. ред. физ.-мат. Лит., 1987. – 176 с.
4. Смирнова И.М., Смирнов В.А. Геометрические задачи с практическим содержанием. – М.: МЦНМО, 2015. – 2-е изд., доп. – 216 с.
5. Екимова М.А., Кукин Г.П. Задачи на разрезание. – М.: МЦНМО, 2002.- 120 с.: ил. Серия: «Секреты преподавания математики»
6. Образовательный портал для подготовки к экзаменам СДАМ ГИА: РЕШУ ОГЭ (Математика). Режим доступа: ОГЭ−2024, Математика: задания, ответы, решения (sdamgia.ru)







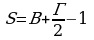 .
.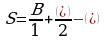 , за ней буква Г, её на второе
, за ней буква Г, её на второе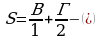 и вспоминаем, что мы на фигуру накинули одну сеть, которую нужно отнять
и вспоминаем, что мы на фигуру накинули одну сеть, которую нужно отнять 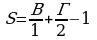 .
. 1.3. Базовые понятия и теоремы
1.3. Базовые понятия и теоремы Квадраты в свою очередь порождают решётку (сетку), а совмещение вершин квадратов образует узлы решётки (сетки). В дальнейшем, площадь одного квадрата сетки мы будем считать равной 1 кв. ед.
Квадраты в свою очередь порождают решётку (сетку), а совмещение вершин квадратов образует узлы решётки (сетки). В дальнейшем, площадь одного квадрата сетки мы будем считать равной 1 кв. ед. Теорема. Все элементарные параллелограммы и треугольники между собой имеют равные площади.
Теорема. Все элементарные параллелограммы и треугольники между собой имеют равные площади.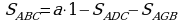 или
или 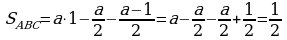 .
. ля вывода формулы рассмотрим произвольный невыпуклый многоугольник у которого
ля вывода формулы рассмотрим произвольный невыпуклый многоугольник у которого 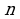 вершин (или как нам привычно - узлов). Узлы на границе фигуры:
вершин (или как нам привычно - узлов). Узлы на границе фигуры: 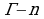 , где Г - это кол-во граничных узлов вместе с вершинами. Буквой N обозначим число элементарных треугольников, на которые мы разбили наш многоугольник. Покажем, что число N не зависит от способа разбиения.
, где Г - это кол-во граничных узлов вместе с вершинами. Буквой N обозначим число элементарных треугольников, на которые мы разбили наш многоугольник. Покажем, что число N не зависит от способа разбиения.  ассмотрим узлы, находящиеся внутри многоугольника, они играют роль вершин треугольников, на которые разбивается многоугольник, заметим, что сумма всех углов, для которых каждая из внутренних точек является вершиной, равна
ассмотрим узлы, находящиеся внутри многоугольника, они играют роль вершин треугольников, на которые разбивается многоугольник, заметим, что сумма всех углов, для которых каждая из внутренних точек является вершиной, равна 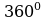 . Получаем, что сумма всех углов всех треугольников с вершинами во внутренних точках равна:
. Получаем, что сумма всех углов всех треугольников с вершинами во внутренних точках равна: 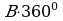 .
. Далее рассмотрим граничные узлы, не являющиеся вершинами, которых
Далее рассмотрим граничные узлы, не являющиеся вершинами, которых 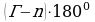 .
. ри вершинах многоугольника, сумма всех углов всех треугольников равна сумме внутренних углов многоугольника, которая вычисляется по известной формуле:
ри вершинах многоугольника, сумма всех углов всех треугольников равна сумме внутренних углов многоугольника, которая вычисляется по известной формуле: 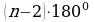 .
.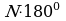 . С другой стороны, учитывая все узлы многоугольника, можно записать равенство:
. С другой стороны, учитывая все узлы многоугольника, можно записать равенство: 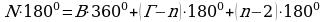 . Преобразовав, получим:
. Преобразовав, получим: 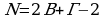 .
.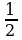 , значит, площадь многоугольника мы с вами найдём из полученной формулы, предварительно разделив её на 2:
, значит, площадь многоугольника мы с вами найдём из полученной формулы, предварительно разделив её на 2: 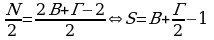 .
.
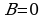 ,
, 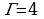 , получаем, что:
, получаем, что: 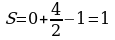 .
. Далее рассмотрим произвольный прямоугольник со сторонами равными a и b. Для начала подсчитаем количество внутренних узлов, для этого обозначим их. Для удобства счёта, перенесём все внутренние узлы, в центры квадратов, для которых любой внутренний узел является верхней левой вершиной.
Далее рассмотрим произвольный прямоугольник со сторонами равными a и b. Для начала подсчитаем количество внутренних узлов, для этого обозначим их. Для удобства счёта, перенесём все внутренние узлы, в центры квадратов, для которых любой внутренний узел является верхней левой вершиной. Теперь можем заметить, что счёт узлов, свёлся к счёту квадратов с узлом внутри. Для этого нам необходимо вычесть столбец и строку, которые не содержат узлы внутри себя. При вычитании строки и столбца мы вычли левую верхнюю клетку (клетка с крестиком) два раза, значит, нам нужно вернуть её один раз. Получаем, что количество внутренних узлов равно:
Теперь можем заметить, что счёт узлов, свёлся к счёту квадратов с узлом внутри. Для этого нам необходимо вычесть столбец и строку, которые не содержат узлы внутри себя. При вычитании строки и столбца мы вычли левую верхнюю клетку (клетка с крестиком) два раза, значит, нам нужно вернуть её один раз. Получаем, что количество внутренних узлов равно: 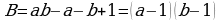 .
. Количество граничных узлов можем посчитать следующим образом. На каждой стороне нашего прямоугольника начиная с верхнего левого узла отметим число узлов, равное длине стороны, в нашем случае
Количество граничных узлов можем посчитать следующим образом. На каждой стороне нашего прямоугольника начиная с верхнего левого узла отметим число узлов, равное длине стороны, в нашем случае 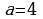 , а
, а 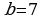 . Получаем, что
. Получаем, что 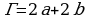 .
.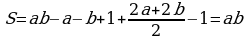 .
. Далее рассмотрим случай для прямоугольного треугольника, получаемого путём разделения прямоугольника любой из своих диагоналей.
Далее рассмотрим случай для прямоугольного треугольника, получаемого путём разделения прямоугольника любой из своих диагоналей. Для начала из прямоугольника уберём все узлы, которые лежат на диагонали, т.к. они являются граничными узлами полученного треугольника. Но убрав все узлы диагонали, мы также убрали узлы, которые являются вершинами треугольника, значит, нам нужно их вернуть. Таким образом получаем, что количество внутренних узлов в прямоугольнике стало равно
Для начала из прямоугольника уберём все узлы, которые лежат на диагонали, т.к. они являются граничными узлами полученного треугольника. Но убрав все узлы диагонали, мы также убрали узлы, которые являются вершинами треугольника, значит, нам нужно их вернуть. Таким образом получаем, что количество внутренних узлов в прямоугольнике стало равно 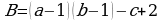 , где c - это количество узлов, лежащих на диагонали (вместе с вершинами прямоугольника!). Так как при разбиении прямоугольника получается два треугольника, то количество внутренних узлов необходимо поделить на два:
, где c - это количество узлов, лежащих на диагонали (вместе с вершинами прямоугольника!). Так как при разбиении прямоугольника получается два треугольника, то количество внутренних узлов необходимо поделить на два: 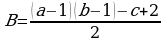 .
. Посчитаем граничные узлы. Для этого рассмотрим треугольник и на каждой стороне обозначим такое число узлов, скольким равна длина стороны. В данном случае
Посчитаем граничные узлы. Для этого рассмотрим треугольник и на каждой стороне обозначим такое число узлов, скольким равна длина стороны. В данном случае 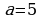 ,
, 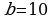 ,
, 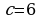 . Если мы начнём обозначать узлы с верхней левой вершины, то обойдя весь треугольник мы увидим, что верхнюю левую вершину мы переобозначили два раза, значит, нам необходимо вычесть одно переобозначение. Получаем, что количество граничных узлов равно:
. Если мы начнём обозначать узлы с верхней левой вершины, то обойдя весь треугольник мы увидим, что верхнюю левую вершину мы переобозначили два раза, значит, нам необходимо вычесть одно переобозначение. Получаем, что количество граничных узлов равно: 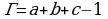 . Подставим:
. Подставим: 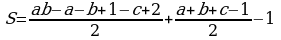 или
или 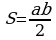 .
. Далее рассмотрим произвольный треугольник. Его площадь можно найти путём вычитания из прямоугольника прямоугольных треугольников. А так как мы доказали справедливость формулы Пика для прямоугольника и прямоугольного треугольника, то формула будет верна и для произвольного треугольника в силу триангуляции (любой треугольник можно разбить на два прямоугольных).
Далее рассмотрим произвольный треугольник. Его площадь можно найти путём вычитания из прямоугольника прямоугольных треугольников. А так как мы доказали справедливость формулы Пика для прямоугольника и прямоугольного треугольника, то формула будет верна и для произвольного треугольника в силу триангуляции (любой треугольник можно разбить на два прямоугольных).




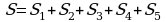 ;
;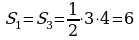 ;
;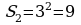 ;
;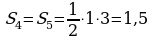 ;
;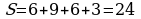 .
.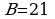 ;
;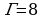 ;
;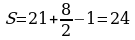 .
.
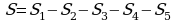 ;
;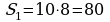 ;
;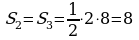 ;
;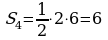 ;
;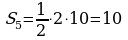 ;
;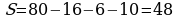 .
.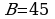 ;
;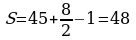 .
.
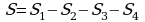 ;
;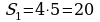 ;
;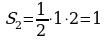 ;
;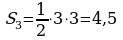 ;
;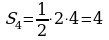 ;
;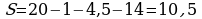 .
.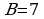 ;
;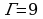 ;
;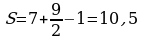 .
.
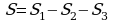 ;
;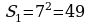 ;
;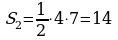 ;
;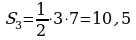 ;
;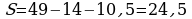 .
.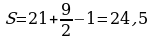 .
.
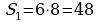 ;
;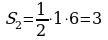 ;
;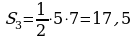 ;
;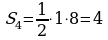 ;
;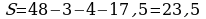 .
.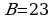 ;
;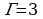 ;
;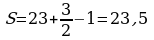 .
.
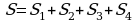 ;
;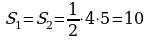 ;
;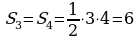 ;
;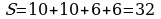 .
.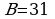 ;
;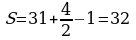 .
.
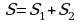 ;
;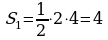 ;
;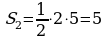 ;
;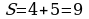 .
.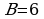 ;
;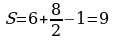 .
.
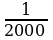 .
. 




















