Статья "Поверхности с постоянной внешней геометрией в Е^6

Поверхности с постоянной внешней геометрией в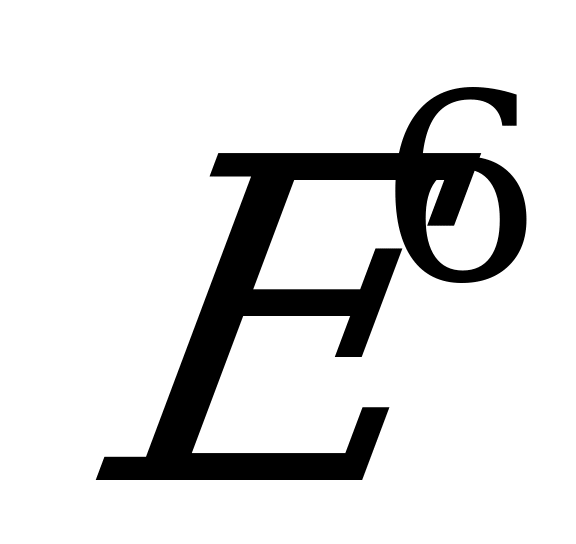

_{Стыций Наталья Анатольевна}

_{Савельев Валерий Михайлович}

_{ГОУ ЛНР «ЛНУ имени Тараса Шевченко}

natali.1977.2011@mail.ru

Вопросы, связанные с изучением подмногообразий евклидова пространства, давно вызывают интерес у геометров. Геометрия подмногообразий является в настоящее время интенсивно развивающейся частью современной геометрии. Первоначально, геометрия подмногообразий была только частью римановой геометрии, но сегодня это есть независимое направление в многомерном обобщении классической теории поверхностей. Геометрия подмногообразий изучает новые факты, не имеющие аналогов в классической теории поверхностей. Она развила новые интересные проблемы вместе с ее специальными методами и имеет много явных и неожиданных связей с механикой и физикой.

Давйте рассмотрим и исследуем пример постоянно изотропного погружения тора 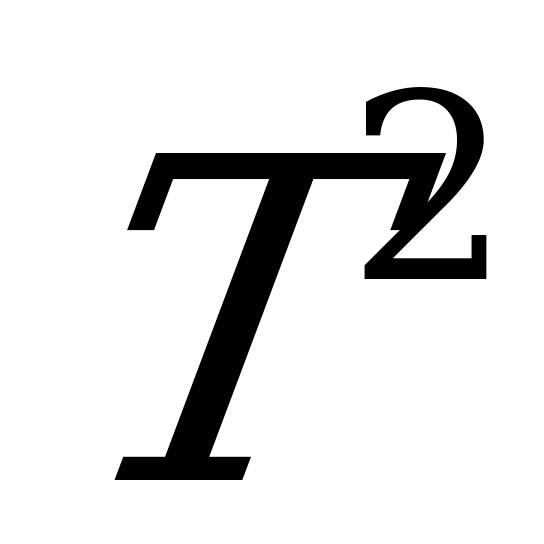в 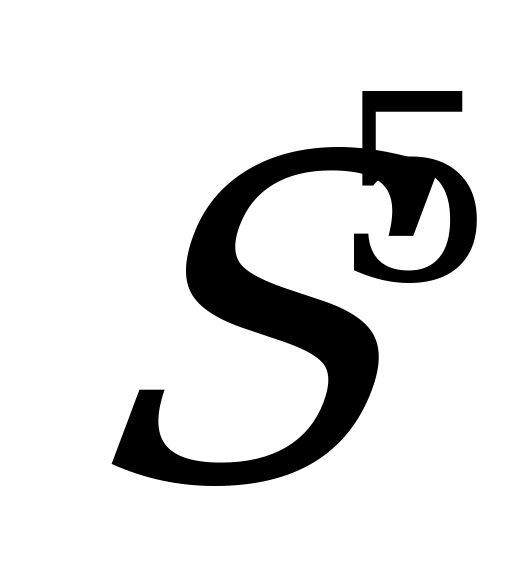. Этот пример возник при изучении стационарных 2-типа поверхностей в сфере (M.Barros,B.Y Chen).

О'Нейл [3] ввел понятие изотропного подмногообразия. Говорят, что подмногообразие 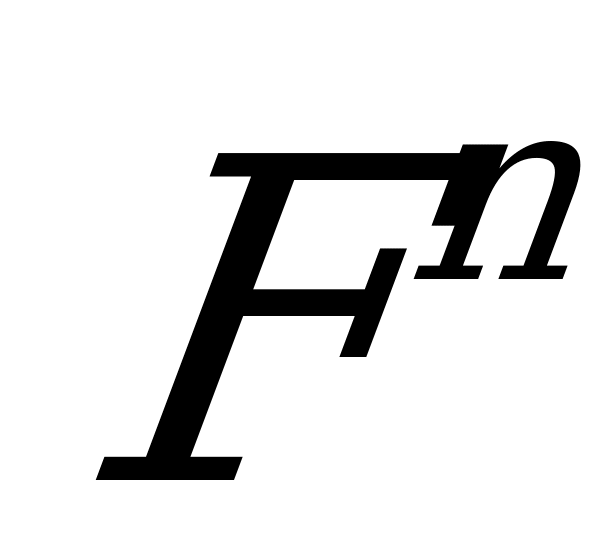есть 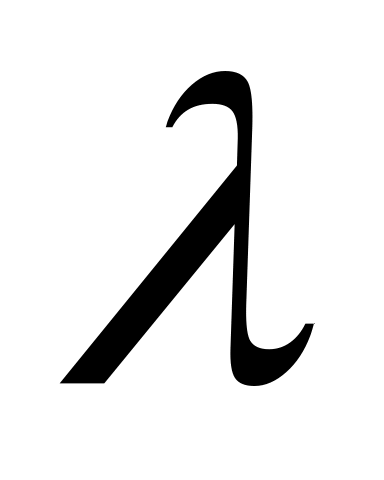- изотропно в точке 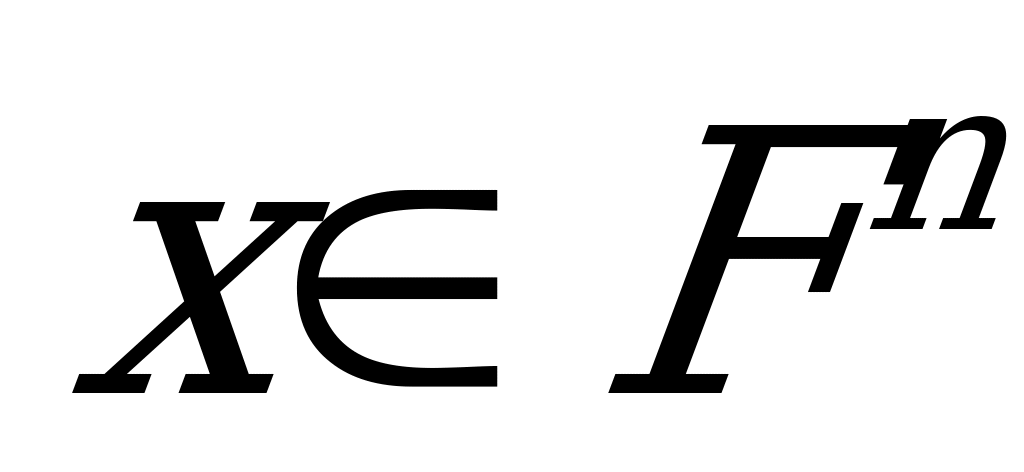, если 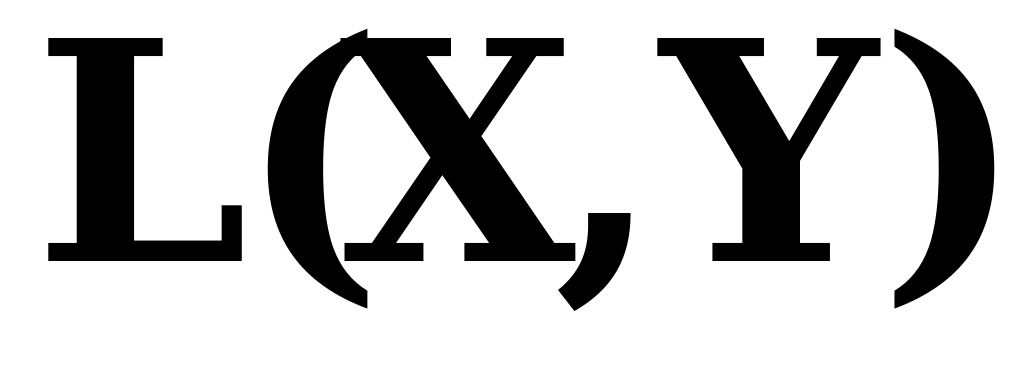имеет одинаковую длину 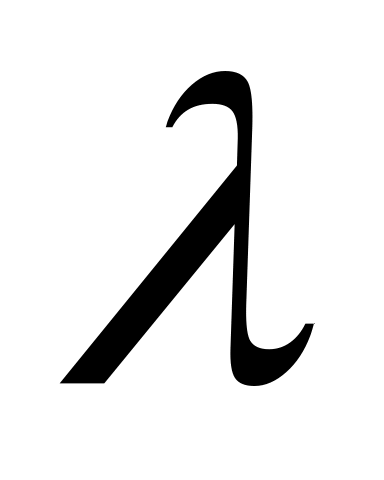для любого единичного касательного вектора 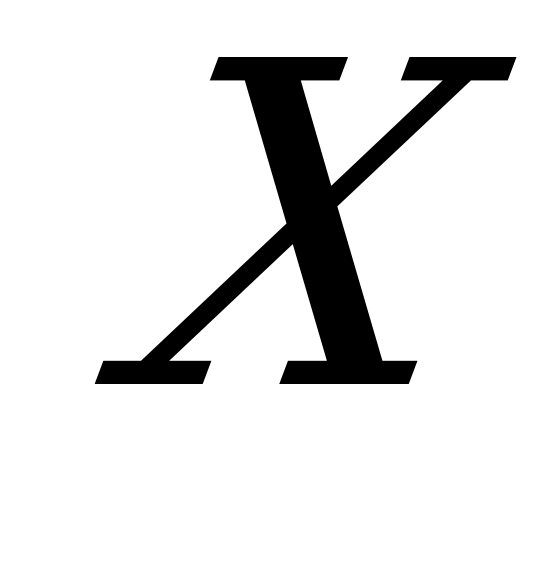в точке 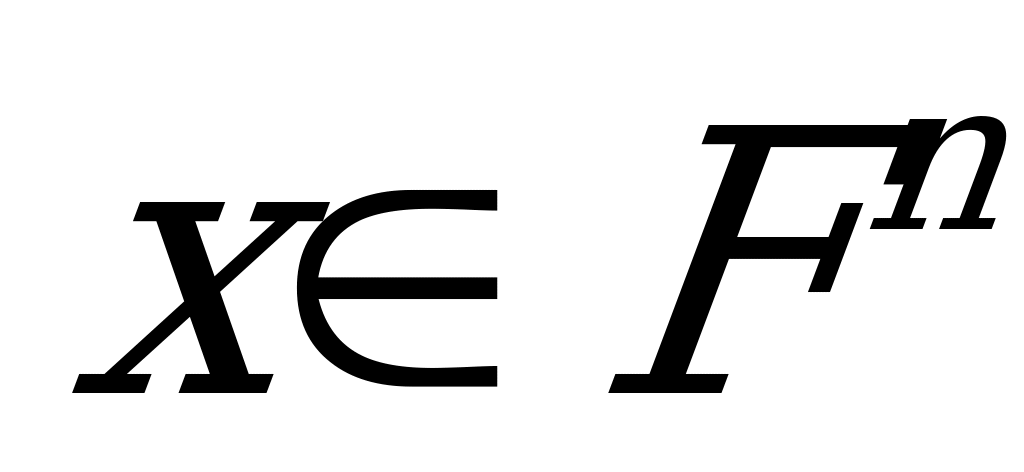Подмногообразие 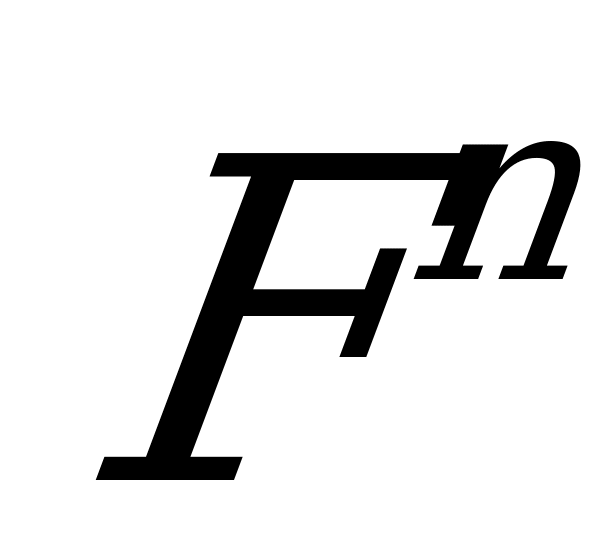изотропно, если оно изотропно в каждой точке.

Таким образом, грассманово отображение двумерного изотропного подмногообразия является конформным. В работе [3] доказывается, что если у изотропного погружения грассманово отображение является конформным и грассманов образ 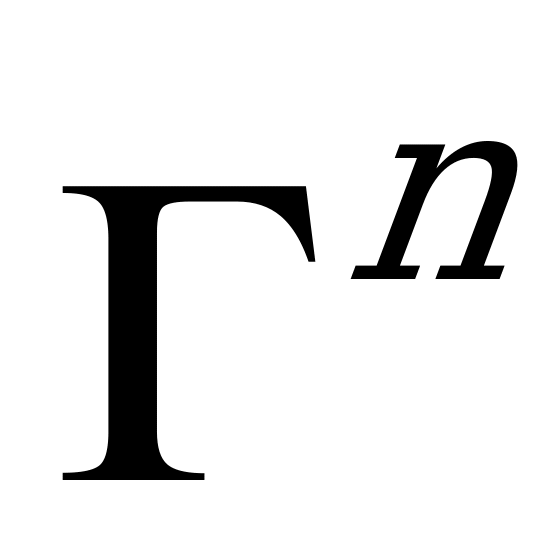вполне омбилическим в 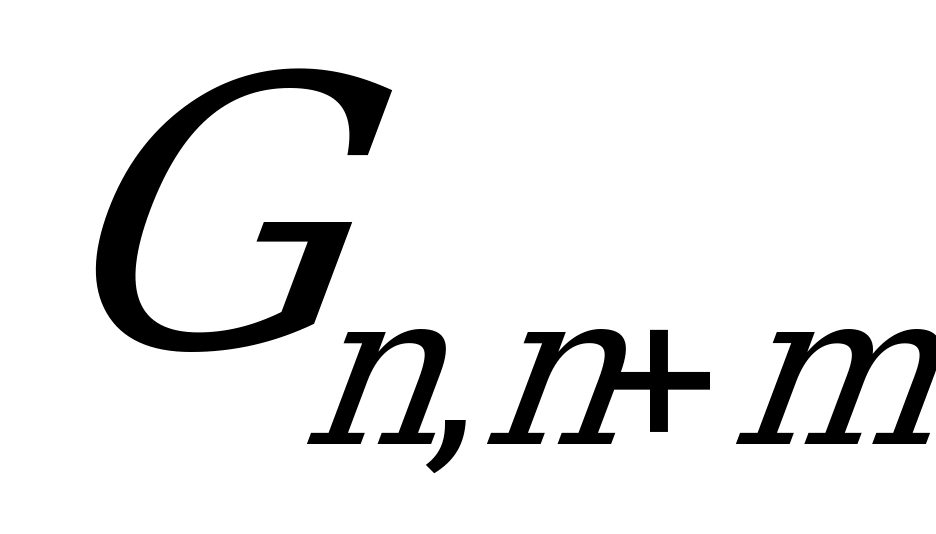,то многообразие 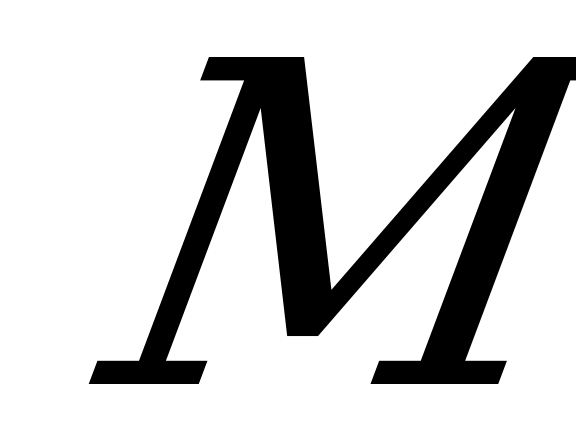погружается в виде минимального и изотропного подмногообразия 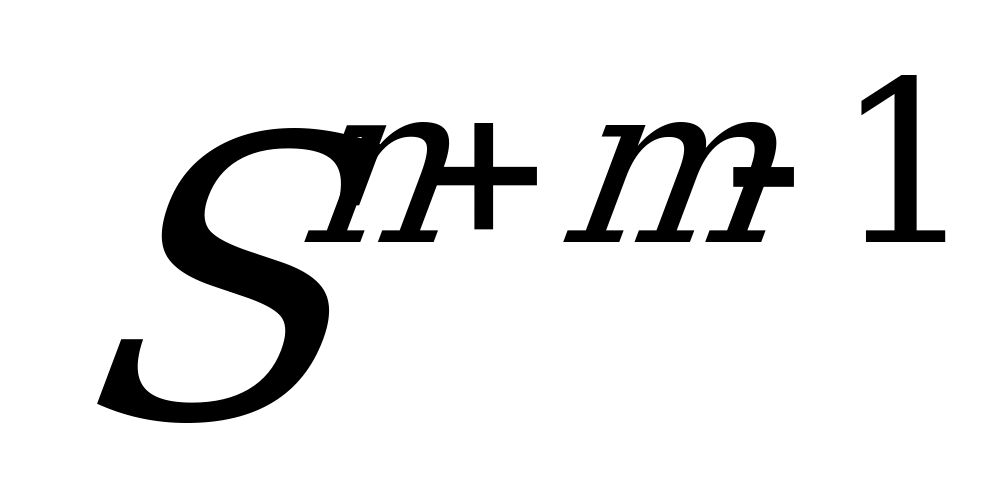в 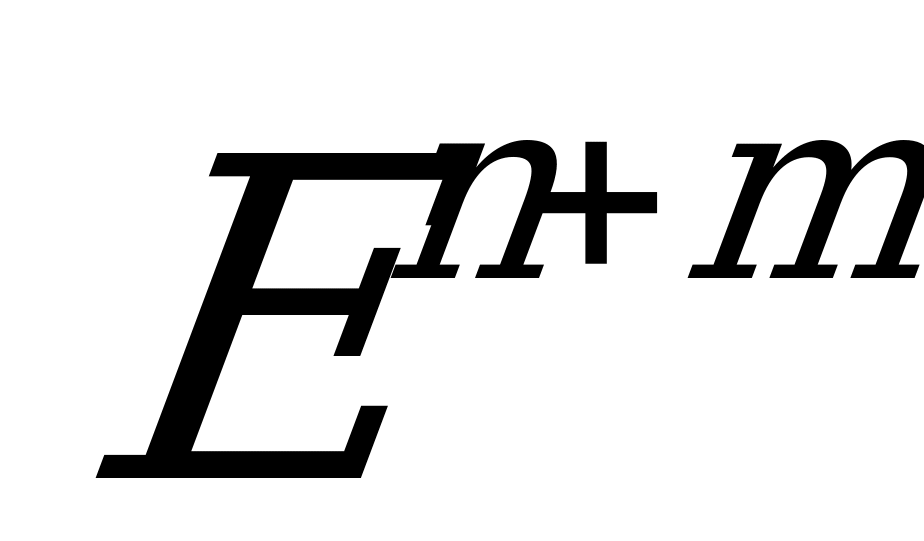, которое имеет параллельную вторую фундаментальную форму.

Произведя все необходимые вычисления получаем, что индикатриса нормальной кривизны искомого постоянного изотропного погружения плоского тора является окружностью радиуса 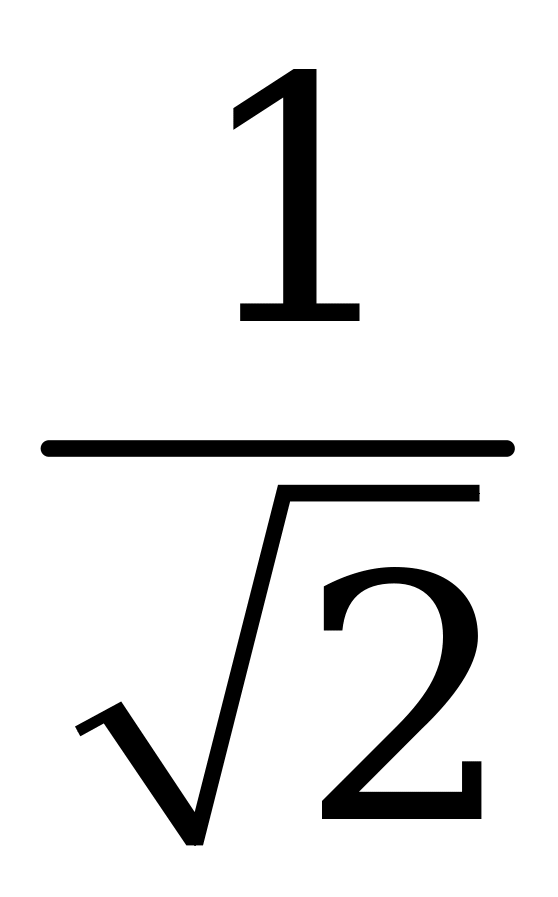. При этом вектор средней кривизны ортогональный плоскости в которой лежит эта окружность. Так что все точки погружения 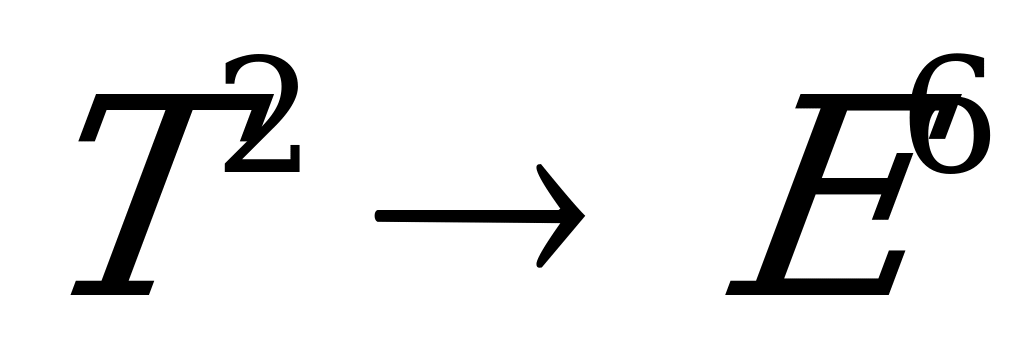есть псевдоомбилическими.

Чен [1] рассматривал спектральные характеристики равнобокого минимального тора. Рассмотрим отображение 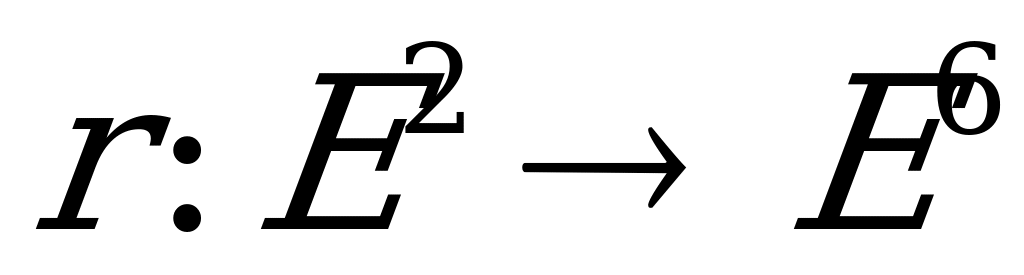, который определяется следующим образом:

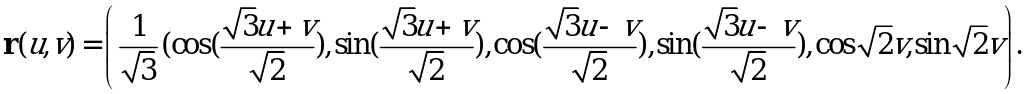Тогда 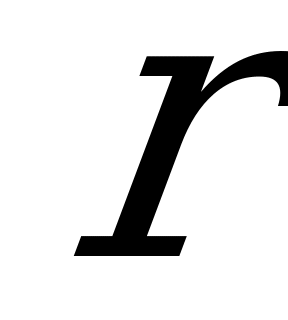задает изометрическое погружение плоского тора 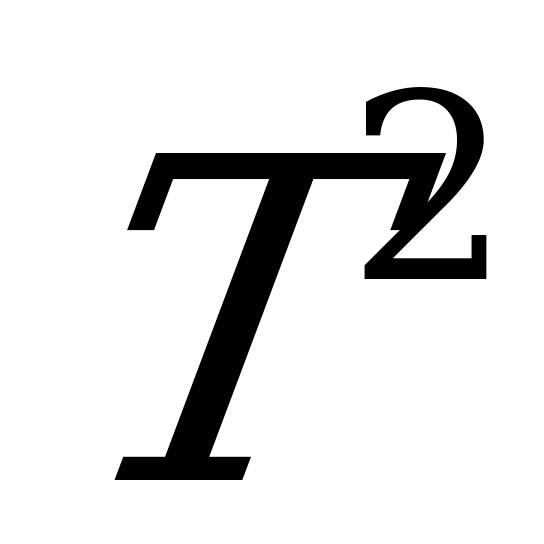в .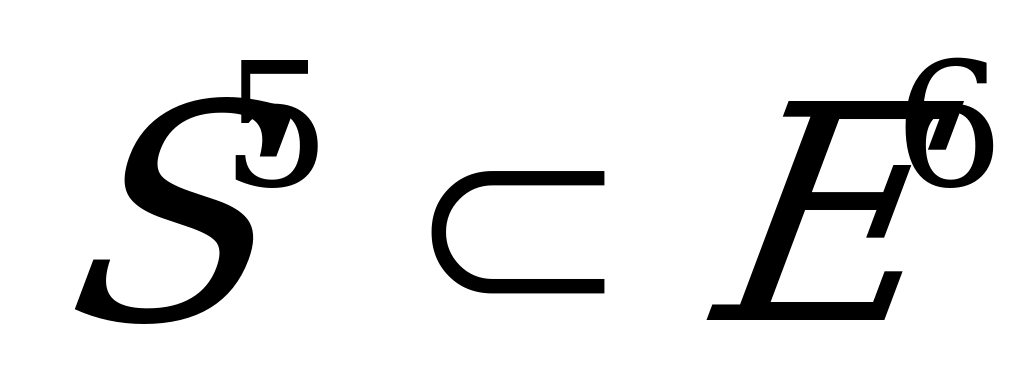

Найдя метрический тензор на 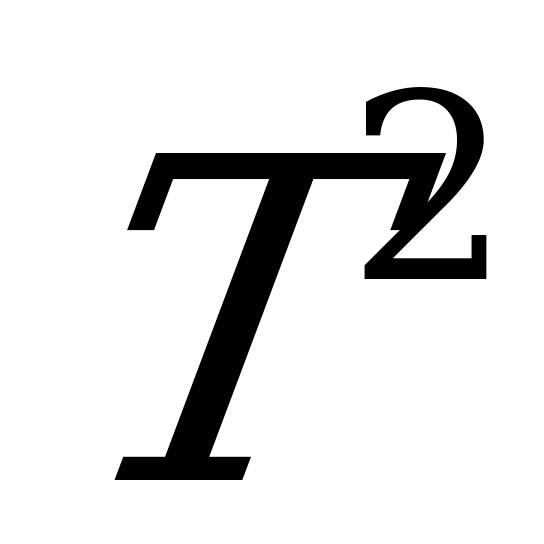установим, что 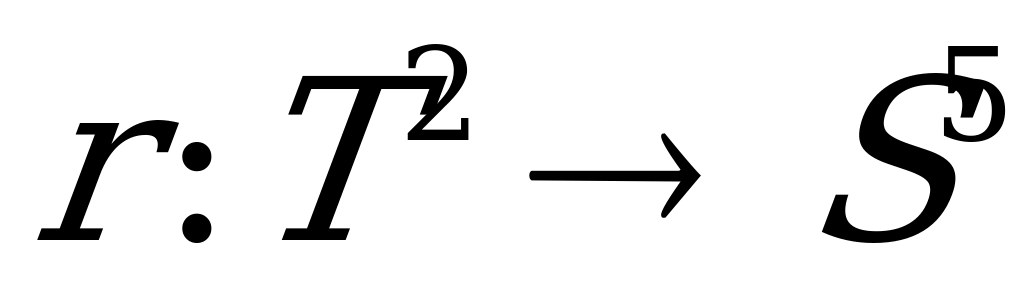есть минимальный плоский тор, который известен, как равнобокий минимальный тор. Исследовав пример изометрического погружения плоского минимального тора 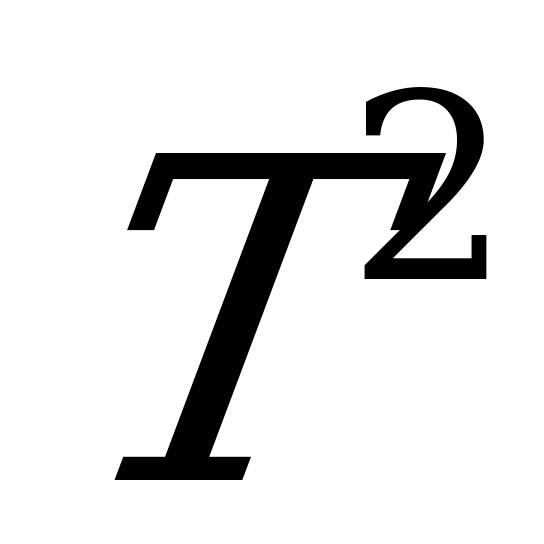в 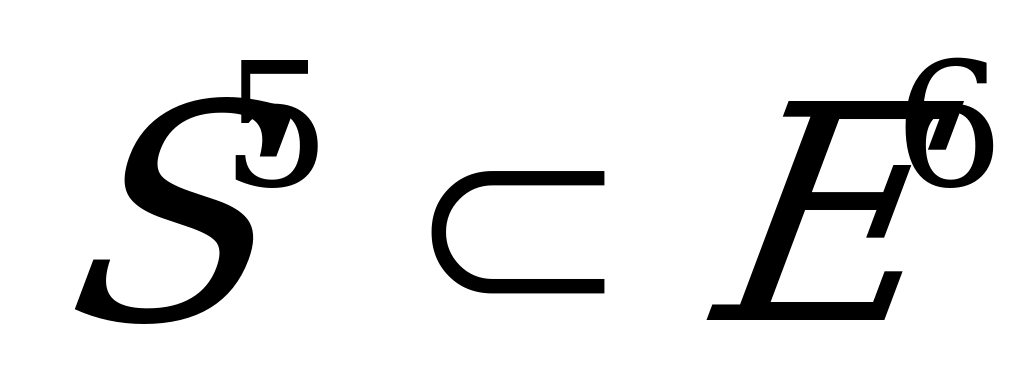, установим, что эллипс нормальной кривизны этого тора является окружностью.

Производя несложные, но громоздкие вычисления можно доказать, что плоская поверхность 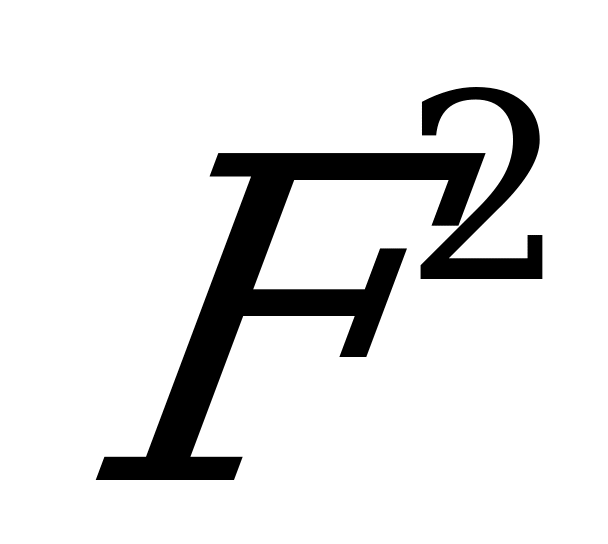в 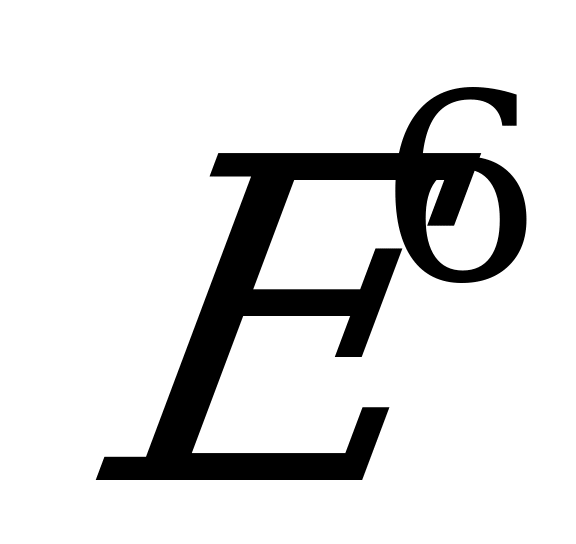[1], которая задает плоский тор погружение которого в  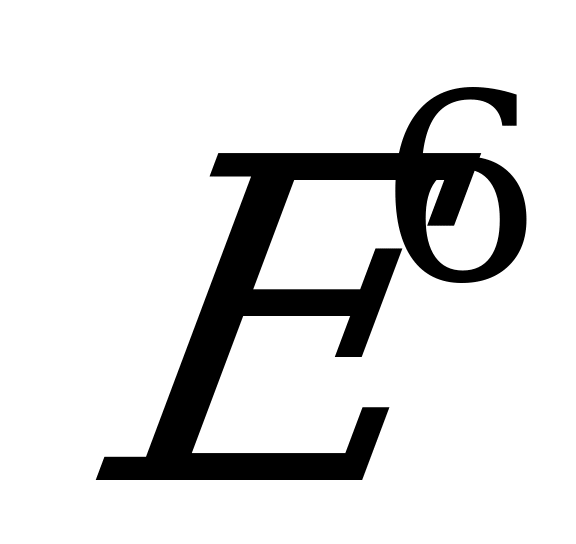конгруэнтно поверхности, имеет контактное число 4. Кроме того установлено, что эллипс нормальной кривизны для этой поверхности является окружностью ненулевого радиуса.

Полученные результаты вычислений могут найти дальнейшее развитие в изучении внешне-геометрических свойств подмногообразий евклидова пространства, в частности, при описании классов поверхностей с постоянной внешней и внутренней геометрией, исследовании таких поверхностей, которые имеют постоянную кривизну грассманова образа. Также эти результаты могут быть использованы для чтения специальных курсов по геометрии подмногообразий, как евклидова пространства так и произвольного риманова пространства.

Библиографический список

1. Аминов Ю. А., Геометрия подмногообразий. – К.: Наукова думка, 2002- – 467 с.

2. Гарибе Т., Поверхности в с постоянной внешней и внутренней геометрией / Т. Гарибе // Укр. геометр. сб. 1981. Вып. 24 С. 12 – 18.

3. Гарибе Т., Двумерные поверхности с постоянной внешней геометрией в 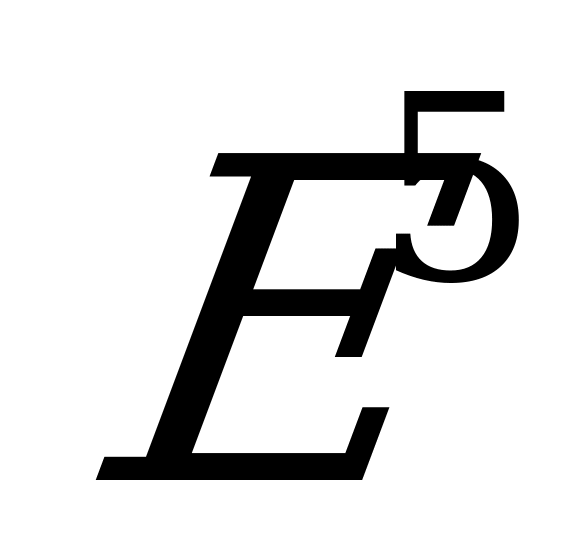/ Т. Гарибе // Укр. геометр. сб. 1982. Вып. 25 С. 11 – 22.

4. Chen, B. Y. What can we do with Nash’s emdedding theorem? – 2004.

5. Chen, B. Y. Differential geometry of rectifying submanifolds, Int. Electron. J. Geom. 9 (2) (2016), 1-8.

6. O'Neill, B. Isotropic and Kaehler submanifolds, Can. J. Math. 17 (1965), 907-915.

7. Sasahara, T. Legendre surfaces in Sasakian space forms whose mean curvature vectors are eigenvectors / T. Sasahara // Publ. Math. Debrecen. – 2005. – 67. – P. 303.

8. Weiner, J.L. On a problem of Chen Willmore etal, Indiana Univ. Math. J., 288 (1979), 99-995.