Министерство науки и высшего образования Российской Федерации федеральное государственное бюджетное общеобразовательное учреждение высшего образования
«Российский экономический университет имени Г.В. Плеханова»
Улан-Баторский филиал
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
Международной научно-практической конференции юных исследователей «Шаг в будущее»
на тему: «Линейные диофантовы уравнения с двумя переменными в олимпиадных задачах»
Выполнил: ученик 8б класса
Жамъяндорж Турбадрах.
Научный руководитель:
Сороковикова В.А., учитель математики
Улан-Батор, 2024
Содержание
Введение …………………………………………………………………………………………... 3
Глава I. Исторический экскурс «Диофант и его уравнения»…………...………………………. 5
Глава II. Теоретические основы ЛДУ с двумя неизвестными …….…………………………… 6
Глава III. Методы и способы решений ЛДУ с двумя переменными…….……………….…….. 9
Решение диофантовых уравнений с помощью цепных дробей ……..…………………….. 9
Решение диофантовых уравнений с помощью перебора вариантов и метода остатков…11
Линейные диофантовы уравнения в экзаменационных задачах МГУ ………..……….… 14
Заключение...……………………………………………………………………………………… 16
Список литературы ……………………………………………………………….……………… 17
Приложение 1. Задачи для самостоятельного решения ……………………….……………….18
Введение
Решение уравнений в целых числах является одной из древнейших математических задач. Наибольшего расцвета эта область математики достигла в Древней Греции.
Задачи на целые числа считаются одними из наиболее сложных задач, предлагаемых учащимся старших классов на профильном ЕГЭ по математике. Так же к решению уравнения в целых числах сводятся решения многих олимпиадных задач по математике. Это объясняется отсутствием универсального метода решения предлагаемых задач. Для их решения надо уметь творчески мыслить, а так же знать основные положения теории чисел, разбираться в вопросах делимости чисел.
Своё знакомство с теорией чисел и теорией делимости, я хочу начать с линейных диофантовых уравнений (ЛДУ) с двумя переменными.
Линейным диофантовым уравнением с двумя переменными называется уравнение вида 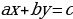 , где (известные) коэффициенты
, где (известные) коэффициенты 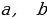 и с – целые числа, причем
и с – целые числа, причем 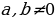 , а неизвестные
, а неизвестные 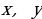 также являются целыми числами.
также являются целыми числами.
Как правило, такие уравнения имеют бесконечное множество решений, поэтому их ещё называют неопределёнными. Диофантовыми эти уравнения стали называть в честь древнегреческого математика Диофанта, который жил в середине III века до н.э.
К решению диофантовых уравнений сводятся разнообразные текстовые задачи, в которых неизвестные величины выражают количество предметов того или иного рода и потому являются натуральными числами. Оказывается, для решения ЛДУ с двумя переменными существуют универсальные методы, но в школе рассматривают только метод перебора, другие методы не изучаются. Поэтому я задался целью изучить некоторые методы их решений. Выбранную тему я считаю для себя актуальной.
Итак, объектом моего исследования являются линейные диофантовы уравнения с двумя переменными.
Гипотеза: Предполагаю, что для решения линейных диофантовых уравнений (ЛДУ) существуют универсальные методы их решения.
Предмет исследования – методы решений ЛДУ с двумя переменными.
Цель моего исследования – разобраться в методах решения линейных диофантовых уравнений с двумя переменными, выявить особенности решения текстовых задач, сводящихся к этим уравнениям..
Исходя из поставленной цели, можно сформулировать следующие задачи:
Познакомиться с биографией Диофанта и историей развития диофантовых уравнений;
Доказать основные теоремы в рамках теории линейных диофантовых уравнений с двумя переменными;
Исследовать случаи, когда уравнение не имеет решений в целых числах;
Рассмотреть методы решений основанные на основных положениях теории чисел;
Выбрать оптимальный метод, освоить его;
Разобрать образцы решения задач, сводящихся к решению линейных диофантовых уравнений с двумя переменными;
Самостоятельно решить ряд задач.
Для решения поставленных задач были использованы следующие методы:
Анализ учебно-методической литературы и интернет-источников;
Анализ контрольно-измерительных материалов ЕГЭ и заданий олимпиад разных лет.
Структура работы обусловлена целью и задачами исследования.
Исследовательская работа состоит из введения, трёх глав, заключения, списка использованных источников, приложения.
Введение раскрывает актуальность, определяет объект, предмет, цель, задачи, методы исследования, теоретическую и практическую значимость работ
Глава первая представляет из себя небольшой исторический экскурс, где я знакомлю с известными биографическими сведениями о Диофанте и его научном труде «Арифметика».
Глава вторая «Теоретические основы линейных диофантовых уравнений с двумя неизвестными» посвящена анализу уравнения вида 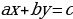 . Здесь выводятся общие формулы для его решения, для соответствующего ему однородного уравнения, также оговаривается, в каких случаях уравнение не имеет решений в целых числах.
. Здесь выводятся общие формулы для его решения, для соответствующего ему однородного уравнения, также оговаривается, в каких случаях уравнение не имеет решений в целых числах.
В третьей главе раскрываются различные методы решения линейных диофантовых уравнений на примере различных задач, в том числе олимпиадных и вступительных в ВУЗ.
В заключении подводятся итоги исследования, формируются окончательные выводы по рассматриваемой теме.
В приложении приведены задачи для самостоятельного решения.
Глава I. Исторический экскурс «Диофант и его уравнения»
История сохранила нам мало черт биографии замечательного древнегреческого ученого-алгебраиста Диофанта, который специализировался на решении задач в целых числах. По некоторым данным Диофант жил до 364 года н.э. Достоверно известно лишь своеобразное жизнеописание Диофанта, которое по преданию было высечено на его надгробии и представляло задачу-головоломку:
«Прах Диофанта гробница покоит; дивись ей и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком.
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругой он обручился.
С нею, пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей.»
Вопрос: Сколько прожил Диофант?
Обозначив за x лет – продолжительность жизни Диофанта, получим следующее уравнение: 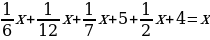 . Решив его, мы получим ответ: 84 года.
. Решив его, мы получим ответ: 84 года.
Жизнь и деятельность Диофанта протекала в Александрии, он собирал и решал известные задачи, а также придумывал новые задачи. Позднее он объединил их в большом труде под названием «Арифметика». Из тринадцати книг, входивших в состав «Арифметики», только шесть сохранились до Средних веков и стали источником вдохновения для математиков эпохи Возрождения.
В этой книге он описал 189 задач, сводящихся к решению уравнений в целых числах. Многие задачи имеют длинную предысторию: некоторые из них восходят к школе Пифагора, другие – к древнему Вавилону. Наиболее известной, решенной Диофантом задача, является задача «о разложении числа на два квадрата». Ее эквивалентом является известная всем теорема Пифагора. До Диофанта задачи такого рода были решены ещё в Древнем Вавилоне около 4 тысяч лет тому назад. Однако, до Диофанта эти задачи трактовались чисто арифметически. Диофант же впервые применил букву для обозначения неизвестной величины. Это был очень важный шаг в создании символического языка математики. Но общепринятым использование буквы для обозначения неизвестных стало только
в XVII-XVIII вв..
Диофант систематизировал и расширил накопленный до него опыт решения неопределенных алгебраических уравнений в целых числах. Каждая из задач была снабжена решением (или несколькими способами решения) и необходимыми пояснениями. Диофант привнес в решение задач новые методы, которые ранее не использовались. «Арифметика» Диофанта легла в основу современной теории чисел. С тех пор уравнения и системы уравнений, которые нужно решить в целых числах стали называться диофантовыми.
Глава II. Теоретические основы линейных диофантовых уравнений с двумя неизвестными
Диофантовыми уравнениями принято называть уравнения с целыми коэффициентами, для которых надо найти целочисленные (или натуральные) решения. При этом количество неизвестных, входящих в уравнение, должно быть не менее двух.
Решить линейное диофантово уравнение означает установить следующее:
имеет ли оно хотя бы одно целочисленное решение;
конечно или бесконечно число его целочисленных решений;
найти все его целочисленные решения.
Рассмотрим уравнение первой степени с двумя неизвестными
| 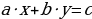 , ,
| (1) |
где 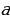 и
и 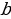 - целые числа, отличные от нуля, а
- целые числа, отличные от нуля, а 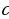 - произвольное целое. Будем считать, что коэффициенты
- произвольное целое. Будем считать, что коэффициенты 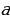 и
и 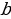 не имеют общих делителей, кроме единицы. Действительно, если наибольший общий делитель этих коэффициентов
не имеют общих делителей, кроме единицы. Действительно, если наибольший общий делитель этих коэффициентов 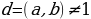 , то справедливы равенства
, то справедливы равенства 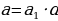 ,
, 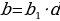 ; уравнение (1) принимает вид
; уравнение (1) принимает вид
и оно может иметь целые решения только в том случае, когда 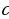 делится на
делится на  . Таким образом, в случае
. Таким образом, в случае 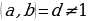 - все коэффициенты уравнения (1) должны делиться нацело на
- все коэффициенты уравнения (1) должны делиться нацело на  , и, сокращая (1) на
, и, сокращая (1) на  , придем к уравнению
, придем к уравнению
| 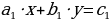 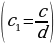 , ,
|
|
коэффициенты которого 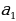 и
и 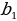 взаимно просты.
взаимно просты.
Рассмотрим сначала случай, когда 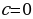 . Уравнение (1) перепишется так:
. Уравнение (1) перепишется так:
| 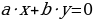 . .
| (1') |
Решая это уравнение относительно 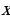 , получим
, получим
| 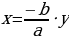 . .
|
|
Ясно, что 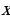 будет принимать целые значения в том и только в том случае, когда
будет принимать целые значения в том и только в том случае, когда 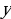 делится на
делится на 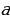 без остатка. Но всякое целое
без остатка. Но всякое целое 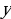 , кратное
, кратное 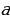 , можно записать в виде
, можно записать в виде
| 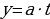 , ,
|
|
где 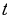 принимает произвольные целые значения
принимает произвольные целые значения 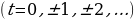 . Подставим это значение
. Подставим это значение  в предыдущее уравнение, тогда
в предыдущее уравнение, тогда
| 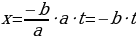 , ,
|
|
и мы получаем формулы, содержащие все целые решения уравнения (1'):
Перейдем теперь к случаю  .
.
Покажем, прежде всего, что для нахождения всех целых решений уравнения (1) достаточно найти какое-нибудь одно его решение, т. е. найти такие целые числа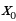 ,
,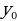 , для которых
, для которых
| 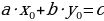 , ,
|
|
Т е о р е м а I. Пусть а и b взаимно просты и 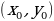 - какое-нибудь решение уравнения
- какое-нибудь решение уравнения
| 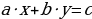 , ,
| (1) |
Тогда формулы
| 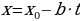 , , 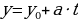
| (2) |
при 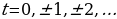 дают все решения уравнения (1).
дают все решения уравнения (1).
Д о к а з а т е л ь с т в о. Пусть 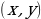 - произвольное решение уравнения (1). Тогда из равенств
- произвольное решение уравнения (1). Тогда из равенств
| 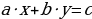 и и 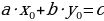
|
|
получаем
| 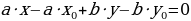 ; ; 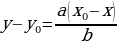 . .
|
|
Так как 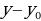 - целое число и числа
- целое число и числа 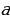 и
и 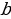 взаимно просты, то
взаимно просты, то 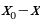 должно нацело делиться на
должно нацело делиться на 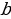 , т. е.
, т. е. 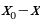 имеет вид
имеет вид
| 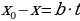 , ,
|
|
где 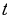 - целое. Но тогда
- целое. Но тогда
| 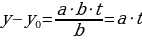 , ,
|
|
и получаем
| 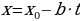 , , 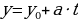 . .
|
|
Таким образом, доказано, что всякое решение 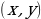 имеет вид (2). Остается еще проверить, что всякая пара чисел
имеет вид (2). Остается еще проверить, что всякая пара чисел 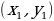 , получаемая по формулам (2) при целом
, получаемая по формулам (2) при целом 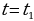 , будет решением уравнения (1). Чтобы провести такую проверку, подставим величины
, будет решением уравнения (1). Чтобы провести такую проверку, подставим величины 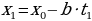 ,
, 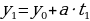 в левую часть уравнения (1):
в левую часть уравнения (1):
| 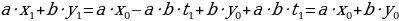 , ,
|
|
но так как 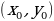 - решение, то
- решение, то 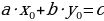 и, следовательно,
и, следовательно, 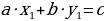 , т.е.
, т.е. 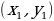 - решение уравнения (1), чем теорема полностью доказана.
- решение уравнения (1), чем теорема полностью доказана.
Итак, если известно одно решение уравнения 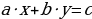 , то все остальные решения найдутся из арифметических прогрессий, общие члены которых имеют вид:
, то все остальные решения найдутся из арифметических прогрессий, общие члены которых имеют вид:
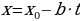 ,
, 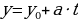
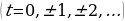
 3аметим, что в случае, когда
3аметим, что в случае, когда 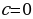 , найденные раньше формулы решений
, найденные раньше формулы решений
| 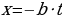 , , 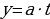
|
|
могут быть получены из только что выведенных формул 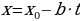 ,
, 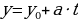 , если выбрать
, если выбрать 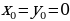 , что можно сделать, так как очевидно, что значения
, что можно сделать, так как очевидно, что значения 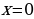 ,
, 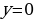 являются решением уравнения
являются решением уравнения
| 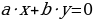 . .
|
|
Как же найти какое-нибудь одно целое решение 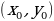 уравнения (1) в случае, когда
уравнения (1) в случае, когда 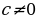 ? Если коэффициенты уравнения не слишком большие числа, то можно попытаться это частное решение найти подбором, а можно использовать различные методы, основанные на теории чисел. Их мы рассмотрим в своей работе далее на примере решения различных задач.
? Если коэффициенты уравнения не слишком большие числа, то можно попытаться это частное решение найти подбором, а можно использовать различные методы, основанные на теории чисел. Их мы рассмотрим в своей работе далее на примере решения различных задач.
Глава III. Методы и способы решения ЛДУ с двумя переменными
Решение ЛДУ с помощью цепных дробей
Пример 1. Решить уравнение 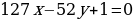 в целых числах.
в целых числах.
Решение: Преобразуем отношение коэффициентов при неизвестных.
Прежде всего, выделим целую часть неправильной дроби 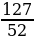 ;
; 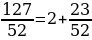
Правильную дробь 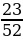 заменим равной ей дробью
заменим равной ей дробью 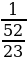 .
.
Тогда получим 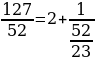 . Проделаем такие же преобразования с полученной в знаменателе неправильной дробью
. Проделаем такие же преобразования с полученной в знаменателе неправильной дробью 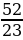 .
.
Теперь исходная дробь примет вид: 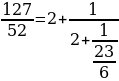
Повторяя те же рассуждения для дроби 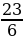 получим
получим 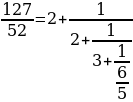 .
.
Выделяя целую часть неправильной дроби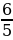 , придем к окончательному результату:
, придем к окончательному результату:
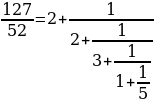
Мы получили выражение, которое называется конечной цепной или непрерывной дробью. Отбросив последнее звено этой цепной дроби - одну пятую, превратим получающуюся при этом новую цепную дробь в простую и вычтем ее из исходной дроби 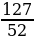 :
:
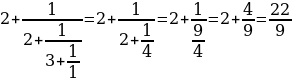 ,
, 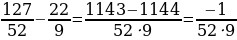 .
.
Приведем полученное выражение к общему знаменателю и отбросим его. Получим:
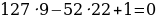 .
.
Из сопоставления полученного равенства с уравнением 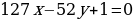 следует, что
следует, что
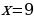 ,
, 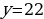 будет решением этого уравнения, и, согласно теореме, все его решения можно записать в виде
будет решением этого уравнения, и, согласно теореме, все его решения можно записать в виде 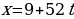 ,
, 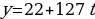 , где
, где 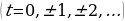 .
.
Ответ: 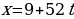 ,
, 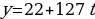 , где
, где 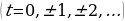 .
.
Полученный результат наводит на мысль о том, что и в общем случае для нахождения решения уравнения 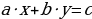 надо разложить отношение коэффициентов при неизвестных в цепную дробь, отбросить ее последнее звено и проделать выкладки, подобные тем, которые были проведены выше. Покажем применение этого вывода на примере 2.
надо разложить отношение коэффициентов при неизвестных в цепную дробь, отбросить ее последнее звено и проделать выкладки, подобные тем, которые были проведены выше. Покажем применение этого вывода на примере 2.
Пример 2. Для перевозки большого количества контейнеров по 170 кг и по 190 кг выделены трёхтонные машины. Можно ли ими загружать машины полностью?
Решение: Пусть x и y – количество контейнеров по 170 и 190 кг соответственно.
Тогда получаем уравнение: 170x + 190y = 3000. После сокращения на 10 уравнение выглядит так: 17x + 19y = 300.
Для нахождения частного решения воспользуемся разложением дроби 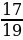 в цепную дробь:
в цепную дробь:
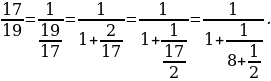
Сворачиваем предпоследнюю подходящую к ней дробь в обыкновенную: 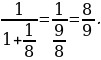
Вычитаем данную дробь из исходной: 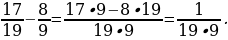
Умножим обе части равенства на 300 и получим частные решения: x = 2700 и y = –2400.
Общее решение уравнения задаётся формулами: x = 2700 – 19t, y = -2400 + 17t.
Учитывая, что x, y 0, находим, что для t должно выполняться условие: 141 t Отсюда получаем, что: t = 142. Следовательно, x = 2, y = 14.
Ответ: да, можно. Потребуется 2 контейнера по 170 кг и 14 по 190 кг.
Решение диофантовых уравнений с помощью
перебора вариантов и метода остатков
Покажем метод перебора вариантов на следующих примерах.
Пример 3. В клетке сидят кролики и фазаны, всего у них 18 ног. Узнать, сколько в клетке тех и других?
Решение: Составим уравнение с двумя неизвестными, в котором х – число кроликов, у – число фазанов: 4x 2y 18, или 2x y 9.
Выразим y через х: y 9 2x.
Далее воспользуемся методом перебора: неположительные значения для x мы брать не можем, так как количество ног не может быть 0 или отрицательным, а также заметим,
что x y получится отрицательным).
Таким образом, задача имеет четыре решения.
Ответ: (1; 7), (2; 5), (3; 3), (4; 1).
Пример 4. Решить в натуральных числах уравнение 5x 8y 39.
Решение: Перепишем уравнение в виде 5x 398y.
Чтобы в условиях задачи уравнение имело смысл, y должен быть меньше или равен 4, но больше 0: 0 y ≤ 4.
Проведем перебор по неизвестной y:
Если y = 1, то 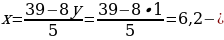 не является натуральным числом.
не является натуральным числом.
Если y = 2, то x = 4,2 – не натуральное число.
Если y = 3, то x = 3 – натуральное число.
Если y = 4, то x = 1,4 – не натуральное число.
Ответ: (3; 3).
Метод остатков. Рассмотрим линейное диофантово уравнение с двумя неизвестными
x, y вида mx ny k, где m, n, k, x, y Z.
Будем считать, что m и n – взаимно простые числа. Если это не так, то всегда можно сократить обе части уравнения на наибольший общий делитель (НОД) чисел m и n, заметим, что если при этом в правой части получится нецелое число, то такое уравнение не будет иметь целых решений.
Далее метод решения зависит от того, насколько большие модули чисел m и n.
Если хотя бы один из коэффициентов невелик по модулю, пусть это будет m, то перепишем уравнение в виде: mx k ny. (1)
Левая часть полученного уравнения (1) делится нацело на m. Значит, должна делиться нацело на m и правая часть этого уравнения. Рассматривая всевозможные остатки l от деления y на m; l 0, 1, ..., m 1, получим, что при одном значении l из указанного промежутка будет делиться на m и правая часть. Поскольку число m невелико по модулю, то и перебор вариантов тоже невелик.
Применение метода остатков покажем на примере решения следующих задач.
Пример 5. При делении на 2 число дает остаток 1, а при делении на 3 – остаток 2. Какой остаток дает это число при делении на 6?
Решение: Так как при делении целого числа на 6 можно получить один из остатков: 0, 1, 2, 3, 4 и 5, то множество целых неотрицательных чисел можно разбить на непересекающиеся подмножества чисел вида 6k , 6k 1, 6k 2, 6k 3 , 6k 4 и 6k 5 , где k = 0, 1, 2, 3, … .
Так как при делении на 2 данное число дает остаток 1, то оно нечетное, поэтому остается рассмотреть числа вида 6k 1, 6k 3 и 6k 5.
Числа вида 6k 1 при делении на 3 дают остаток 1, числа вида 6k 3 кратны 3 и только числа вида 6k 5 при делении на 3 дают остаток 2. Следовательно, число имеет вид 6k 5, т.е. при делении на 6 даёт остаток 5.
Ответ: Если при делении на 2 число дает остаток 1, а при делении на 3 – остаток 2, то при делении на 6 это число даёт остаток 5.
Пример 6. Пусть число p 3 является простым.
Доказать, что: а) имеет место представление p 6k 1 для некоторого k N;
б) 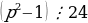 .
.
Решение: а) Рассуждения проводим по остаткам при делении на 6. Все натуральные числа распадаются на 6 классов 6k,6k 1,6k 2,6k 3,6k 4,6k 5. Т.к. числа первого класса делятся на 2, 3, поэтому они составные. Числа третьего класса делятся на 2, числа четвертого класса делятся на 3, числа пятого класса делятся на 2. Простое число p может попасть только либо в класс 6k 1, либо в класс 6k 5 6k 1.
Что и требовалось доказать.
б) Т.к. p 6k 1, то 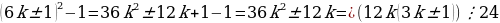 , т.к. первый множитель делится на 12, а третий на 2. Что и требовалось доказать.
, т.к. первый множитель делится на 12, а третий на 2. Что и требовалось доказать.
Пример 7. Тане в 1999 году исполнилось столько лет, какова сумма цифр года её рождения. В каком году она родилась?
Решение: Сумма цифр года рождения людей, родившихся в 19 веке, не превышает 28. Поэтому Таня могла родиться только в 20-м веке. Таким образом, имеем:
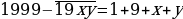
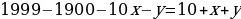
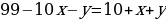
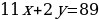
Решим это уравнение применяя метод остатков.
Перепишем уравнение в виде: 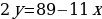 . Поскольку левая часть уравнения делится на 2, то и правая часть должна делиться на 2. Рассмотрим 2 случая:
. Поскольку левая часть уравнения делится на 2, то и правая часть должна делиться на 2. Рассмотрим 2 случая:
Если 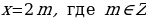 , то
, то 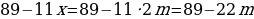 - не делится на 2.
- не делится на 2.
Если 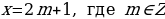 , то
, то 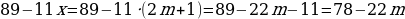 - делится на 2.
- делится на 2.
Таким образом, 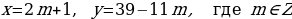 .
.
Учитывая, что 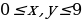 , получаем
, получаем
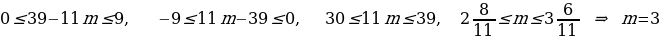 .
.
Отсюда, 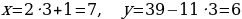 .
.
Ответ: Таня родилась в 1976 году.
Пример 8. Есть ли в нашей школе ученики, которым в 2024 году исполнится столько лет, какова сумма цифр года рождения?
Решение: Ученики нашей школы могли родиться только в 21-м веке.
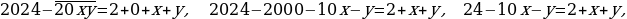
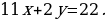
Легко угадываются все возможные целые решения этого уравнения.
Их всего два: (0; 11), (2; 0). При этом решение (0; 11) – не удовлетворяет условию 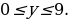
Таким образом, в 2024 году детям, рождённым в 2020 году исполнится столько лет, какова сумма цифр их года рождения, то есть 2 + 0 + 2 + 0 = 4 года. Это слишком мало, чтобы быть учениками нашей школы.
Ответ: таких учеников в школе нет.
Пример 9. Найдите все целые решения уравнения 3x – 12y = 7.
Решение: Левая часть делится на 3, а правая не делится. Поэтому решений нет.
Ответ: нет решений.
Диофантовы уравнения в экзаменационных задачах МГУ
В данной главе я рассмотрю несколько задач, предложенных для самостоятельного решения в книге [3, с. 29]. Эти задачи предлагались на вступительных экзаменах в МГУ им. М. И. Ломоносова в разные годы.
Задача 3.1. (Экономический факультет, 1994, №1.) Найдите все целочисленные решения системы 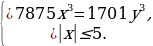
Решение: Разложим коэффициенты уравнения системы на простые множители и найдём их наибольший общий делитель:
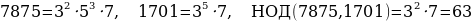 .
.
Сократим уравнение на 63 и получим: 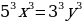 или
или 
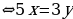 . Замечаем, что левая часть уравнения должна делиться на 3, а правая – на 5. Это возможно только в том случае, если х кратно трём, а y – пяти, т.е. х=3t, y=5t, где t – целое число.
. Замечаем, что левая часть уравнения должна делиться на 3, а правая – на 5. Это возможно только в том случае, если х кратно трём, а y – пяти, т.е. х=3t, y=5t, где t – целое число.
Учитывая неравенство системы, получаем: х = -3, 0, 3. Отсюда, y = -5, 0, 5.
Ответ: (-3; -5), (0; 0), (3; 5).
Задача 3.2. (Факультет государственного управления, 2004, июль, №4.) Компания предложила 350 своим служащим выполнить сверхурочную работу, причем каждому мужчине предлагалось в виде вознаграждения 20 долларов, а женщине –
16 долларов 30 центов. Все женщины согласились с этим предложением, а часть мужчин отказалась. Общая сумма выплаченного вознаграждения составила 5705 долларов. Какова сумма вознаграждения, выплаченного всем женщинам?
Решение: Пусть х – мужчин и y – женщин согласились на сверхурочную работу. Тогда имеем уравнение: 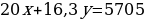 или
или 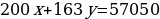 .
.
Решим это уравнение методом «спуска». Для этого выразим из этого уравнения переменную y, имеющую меньший коэффициент. Получим:
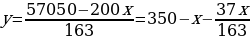 . Так как y – целое число, то должно быть целым выражение
. Так как y – целое число, то должно быть целым выражение 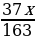 , т.е.
, т.е. 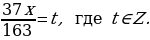 Имеем
Имеем 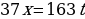 . Аналогично выразим переменную х:
. Аналогично выразим переменную х: 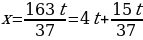 . Обозначим
. Обозначим 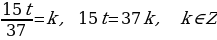 . Продолжим этот процесс:
. Продолжим этот процесс: 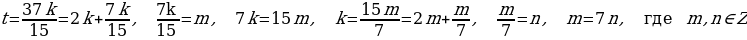 .
.
Теперь начинаем последовательно возвращаться к переменным х и y.
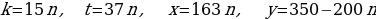 .
.
Если n = 0, то 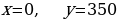 – не удовлетворяет смыслу задачи, так как в задаче предполагается наличие служащих мужчин.
– не удовлетворяет смыслу задачи, так как в задаче предполагается наличие служащих мужчин.
Если n = 1, то 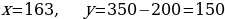 – решение вполне удовлетворяет.
– решение вполне удовлетворяет.
При n = 2 и более получатся решения, не удовлетворяющие смыслу задачи.
Таким образом, 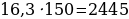 долларов – сумма вознаграждения, выплаченного женщинам.
долларов – сумма вознаграждения, выплаченного женщинам.
Ответ: 2445.
Задача 3.3. (Социологический факультет, 2006, №4.) Накануне экзамена Лиза и её товарищ искали на Воробьёвых горах четырёхлистный клевер, приносящий, по народной примете, удачу. В первый день товарищ нашел четырехлистников на 20% больше, чем Лиза. Во второй день, наоборот, на 30% меньше, чем Лиза в этот день. Всего за два дня Лиза нашла на 10% больше, чем её товарищ. Какое минимальное количество четырехлистников могли найти студенты при данных условиях?
Решение: Оформим условие задачи в таблицу
|
| Найдено клеверов
в I день | Найдено клеверов
во II день | Всего за два дня |
| Лиза | 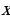
| 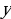
| 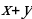
|
| Товарищ | 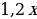
| 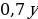
| 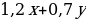
|
Зная, что Лиза за два дня нашла четырехлистников на 10% больше, чем её товарищ, получаем уравнение: 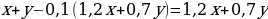 .
.
Раскрыв скобки и приведя подобные слагаемые, получаем: 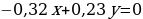 или
или 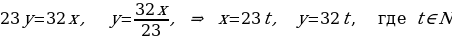 .
.
Чтобы получить ответ на вопрос задачи составим новую таблицу:
| t | 1 | 2 | 3 | 4 | 5 |
| 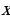
| 23 | 46 | 69 | 92 | 115 |
| 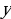
| 32 | 64 | 96 | 128 | 160 |
| 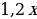
| 27,6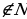 | 55,2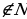 | 82,8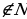 | 110,4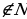 | 138 |
| 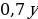
|
|
|
|
| 112 |
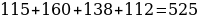 – минимальное количество четырехлистников могли найти студенты при данных условиях.
– минимальное количество четырехлистников могли найти студенты при данных условиях.
Ответ: 525.
Заключение
В ходе исследования я пришел к следующим результатам:
ЛДУ ax+by=c имеет решение, если свободный член делится на наибольший общий делитель коэффициентов уравнения при неизвестных x и y. Эти решения можно записать в общем виде: x= x0-bt, y= y0+at, где t – целое число, а (x0, y0) – частное решение данного уравнения
ЛДУ с двумя переменными не имеет решений тогда, когда коэффициенты уравнения при неизвестных не взаимно просты, а число c при этом не делится на их наибольший общий делитель.
Например, уравнение 12x + 3y = 5 не имеет решений, т.к. 5 не делится на число 3, которое является наибольшим общим делителем чисел 12 и 3.
Универсальный метод решения ЛДУ заключается в том, чтобы в начале найти хотя бы одно какое-нибудь частное решение. Зная частное решения, можно получить общие формулы.
Частные решения можно найти различными способами, например:
С помощью цепных дробей;
Методом «спуска», его ещё называют методом измельчения или рассеивания;
Выражая одну переменную через другую и выделяя целую часть.
Разобрав методы решения линейных уравнений в целых числах, для себя я сделал следующие выводы:
Метод остатков удобно применять тогда, когда хотя бы один из коэффициентов уравнения небольшой.
С помощью метода «спуска» и с помощью цепных дробей легко находить частные решения, а далее использовать общие формулы. Но минус в том, что формулы можно забыть.
Метод выделения целой части из дроби хорош тем, что мы сразу приходим к общему решению. Поэтому он мне нравится больше всех и большинство блогеров показывают именно этот метод.
Для решения диофантовых уравнений высших степеней применяют другие методы,
а именно: метод разложения на множители, метод оценки, решение уравнения с двумя переменными как квадратного относительно одной из переменных, но это может стать темой моего следующего исследования.
Выполняя работу, я узнал что такое диофантово уравнение и научился решать его разными способами. Мною было разобрано и решено много интересных задач. В процессе работы, я узнал что такое цепная дробь, научился представлять обыкновенную дробь в виде цепной дроби и находить с её помощью частное решение.
Надеюсь, что полученные в ходе выполнения работы знания и умения, мне пригодятся при решении олимпиадных задач. Считаю, что гипотеза подтвердилась и цели исследования достигнуты.
Список литературы и интернет-источников
Гринько Е.П., Головач А.Г. Учебно-методическое пособие: Методы решения диофантовых уравнений при подготовке школьников к олимпиадам. – Брест, 2013.
Корянов А.Г. Математика. ЕГЭ 2010. Задания С6. Уравнения в целых числах (от учебных задач до олимпиадных задач).
Линейные диофантовы уравнения / Г. Фалин, А. Фалин. – М.: Чистые пруды, 2008. – 32 с. – (Библиотечка «Первого сентября», серия «Математика». Вып. 24).
https://math100.ru/ - сайт для подготовки к ОГЭ и ЕГЭ по математике.
https://problems.ru/ - сайт с олимпиадными задачами.
https://www.youtube.com/watch?v=8KTw1-5aWfs – объяснение метода выделения целой части из дроби
Приложение 1.
Задачи для самостоятельного решения
Решите в целых числах уравнение:
а) 7х + 11у = 69; б) 3х + 17у = 143;
в) 5х + 29у = 39; г) 7х + 31у = 90;
д) 107x 84y 1; е) 17x 13y 5; ж) 3x + 5y = 7
Решите в натуральных числах уравнение: а) x + у = 11; б) 3х + 5у = 17.
Докажите, что прямая 4х + 6у – 7 = 0 не проходит через точки, обе координаты которых – целые числа.
Найдите наименьшее c, при котором
а) уравнение 7x + 9y = c имело бы ровно шесть натуральных решений;
б) уравнение 14x + 11y = c имело бы ровно пять натуральных решений.
Представьте дробь в виде цепной дроби: а) 7/11; б) 3/8; в) 9/5; г) 17/3.
Решить способом измельчения в целых числах уравнение:
а) 5х + 8у = 39; б) 7х + 11у = 43.
Найти число, которое при делении на 3 дает остаток 2, при делении на 5 – остаток 3, а при делении на 7 – остаток 2.
Шалтай-Болтай ходит по прямой, проходя за минуту либо 37 шагов влево, либо
47 шагов вправо. За какое наименьшее время он может оказаться на один шаг правее исходной точки?
Кузнечик прыгает вдоль координатного луча попеременно: на 5 единичных отрезков вправо и на 3 единичных отрезка влево. Сможет ли он за несколько прыжков из
точки 0 попасть: а) в точку 6; б) в точку 7?
У кассира есть только 72-рублевые купюры, а у вас – только 105-рублевые (у обоих
в неограниченном количестве).
а) Сможете ли вы уплатить кассиру один рубль?
б) А 3 рубля?
Жители города Глупова пользуются купюрами только в 35 и 80 тыров. Сможет ли рассчитаться продавец с покупателем, который хочет купить:
шоколадку за 57 тыров;
б) булочку за 15 тыров?
У Гарри Поттера имеются двое песочных часов: на 7 минут и на 11 минут. Волшебное зелье должно варится 15 минут. Как сварить его Гарри Поттеру, повернув часы минимальное кол-во раз? Сколько раз переворачиваем часы?







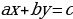 , где (известные) коэффициенты
, где (известные) коэффициенты 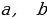 и с – целые числа, причем
и с – целые числа, причем 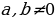 , а неизвестные
, а неизвестные 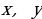 также являются целыми числами.
также являются целыми числами. 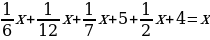 . Решив его, мы получим ответ: 84 года.
. Решив его, мы получим ответ: 84 года.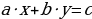 ,
,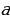 и
и 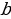 - целые числа, отличные от нуля, а
- целые числа, отличные от нуля, а 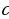 - произвольное целое. Будем считать, что коэффициенты
- произвольное целое. Будем считать, что коэффициенты 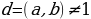 , то справедливы равенства
, то справедливы равенства 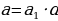 ,
, 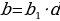 ; уравнение (1) принимает вид
; уравнение (1) принимает вид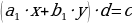
 . Таким образом, в случае
. Таким образом, в случае 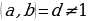 - все коэффициенты уравнения (1) должны делиться нацело на
- все коэффициенты уравнения (1) должны делиться нацело на 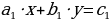
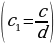 ,
,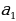 и
и 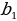 взаимно просты.
взаимно просты.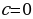 . Уравнение (1) перепишется так:
. Уравнение (1) перепишется так: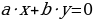 .
.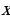 , получим
, получим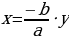 .
.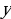 делится на
делится на 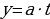 ,
,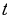 принимает произвольные целые значения
принимает произвольные целые значения 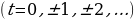 . Подставим это значение
. Подставим это значение 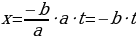 ,
,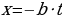 ,
, 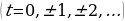 .
.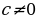 .
.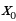 ,
,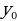 , для которых
, для которых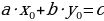 ,
,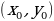 - какое-нибудь решение уравнения
- какое-нибудь решение уравнения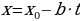 ,
, 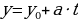
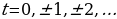 дают все решения уравнения (1).
дают все решения уравнения (1).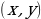 - произвольное решение уравнения (1). Тогда из равенств
- произвольное решение уравнения (1). Тогда из равенств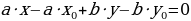 ;
; 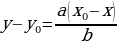 .
.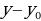 - целое число и числа
- целое число и числа 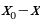 должно нацело делиться на
должно нацело делиться на 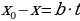 ,
,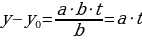 ,
,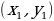 , получаемая по формулам (2) при целом
, получаемая по формулам (2) при целом 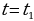 , будет решением уравнения (1). Чтобы провести такую проверку, подставим величины
, будет решением уравнения (1). Чтобы провести такую проверку, подставим величины 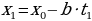 ,
, 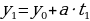 в левую часть уравнения (1):
в левую часть уравнения (1):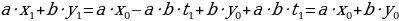 ,
,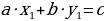 , т.е.
, т.е.  3аметим, что в случае, когда
3аметим, что в случае, когда 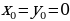 , что можно сделать, так как очевидно, что значения
, что можно сделать, так как очевидно, что значения 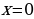 ,
, 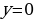 являются решением уравнения
являются решением уравнения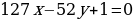 в целых числах.
в целых числах.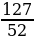 ;
; 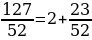
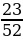 заменим равной ей дробью
заменим равной ей дробью 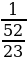 .
.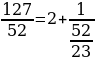 . Проделаем такие же преобразования с полученной в знаменателе неправильной дробью
. Проделаем такие же преобразования с полученной в знаменателе неправильной дробью 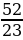 .
. 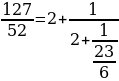
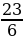 получим
получим 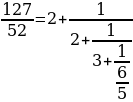 .
.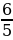 , придем к окончательному результату:
, придем к окончательному результату: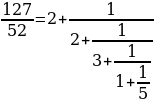
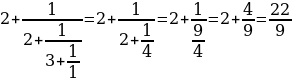 ,
, 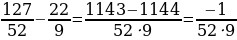 .
.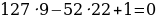 .
.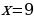 ,
, 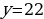 будет решением этого уравнения, и, согласно теореме, все его решения можно записать в виде
будет решением этого уравнения, и, согласно теореме, все его решения можно записать в виде 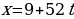 ,
, 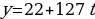 , где
, где 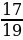 в цепную дробь:
в цепную дробь: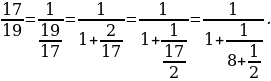
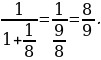
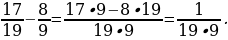
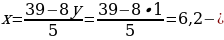 не является натуральным числом.
не является натуральным числом. 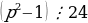 .
.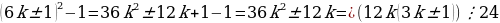 , т.к. первый множитель делится на 12, а третий на 2. Что и требовалось доказать.
, т.к. первый множитель делится на 12, а третий на 2. Что и требовалось доказать. 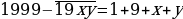
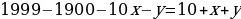
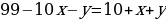
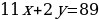
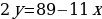 . Поскольку левая часть уравнения делится на 2, то и правая часть должна делиться на 2. Рассмотрим 2 случая:
. Поскольку левая часть уравнения делится на 2, то и правая часть должна делиться на 2. Рассмотрим 2 случая: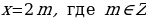 , то
, то 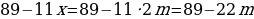 - не делится на 2.
- не делится на 2.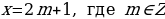 , то
, то 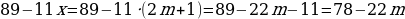 - делится на 2.
- делится на 2.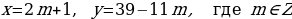 .
.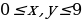 , получаем
, получаем 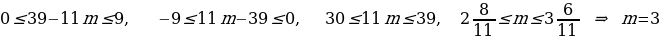 .
.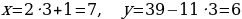 .
.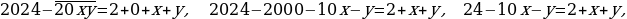
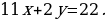
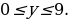
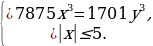
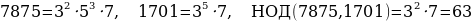 .
.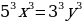 или
или 
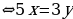 . Замечаем, что левая часть уравнения должна делиться на 3, а правая – на 5. Это возможно только в том случае, если х кратно трём, а y – пяти, т.е. х=3t, y=5t, где t – целое число.
. Замечаем, что левая часть уравнения должна делиться на 3, а правая – на 5. Это возможно только в том случае, если х кратно трём, а y – пяти, т.е. х=3t, y=5t, где t – целое число. 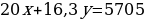 или
или 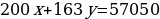 .
.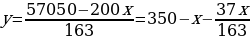 . Так как y – целое число, то должно быть целым выражение
. Так как y – целое число, то должно быть целым выражение 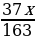 , т.е.
, т.е. 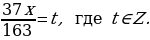 Имеем
Имеем 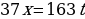 . Аналогично выразим переменную х:
. Аналогично выразим переменную х: 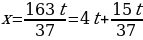 . Обозначим
. Обозначим 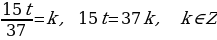 . Продолжим этот процесс:
. Продолжим этот процесс: 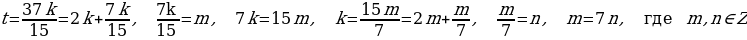 .
.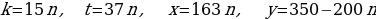 .
.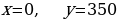 – не удовлетворяет смыслу задачи, так как в задаче предполагается наличие служащих мужчин.
– не удовлетворяет смыслу задачи, так как в задаче предполагается наличие служащих мужчин.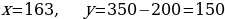 – решение вполне удовлетворяет.
– решение вполне удовлетворяет.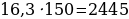 долларов – сумма вознаграждения, выплаченного женщинам.
долларов – сумма вознаграждения, выплаченного женщинам.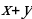
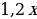
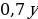
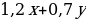
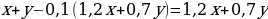 .
.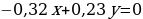 или
или 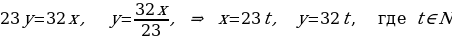 .
.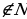
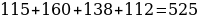 – минимальное количество четырехлистников могли найти студенты при данных условиях.
– минимальное количество четырехлистников могли найти студенты при данных условиях.
















